| Term | Definition | Section of Book |
|---|
| abbreviated electron configuration | An electron configuration that uses one of the noble gases to represent the core of electrons up to that element. | Organization of Electrons in Atoms |
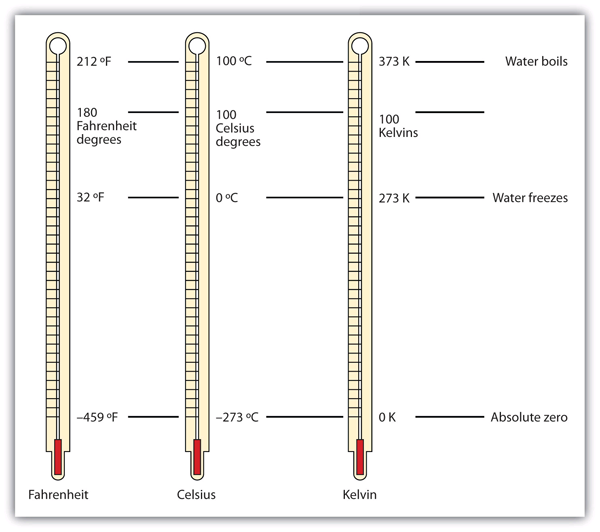
| absolute zero | The minimum possible temperature, labeled 0 K (zero kelvins) | Other Units: Temperature and Density |
| acid | An ionic compound of the H+ cation dissolved in water | Acids |
| acid | A compound that increases the amount of H+ ions in an aqueous solution | Neutralization Reactions |
| acid dissociation constant (Ka) | The equilibrium constant for the dissociation of a weak acid into ions | Some Special Types of Equilibria |
| acid salt | An ionic compound whose aqueous solution is slightly acidic | Strong and Weak Acids and Bases and Their Salts |
| activated complex | See transition state | Reaction Mechanisms |
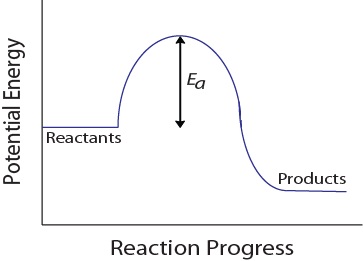
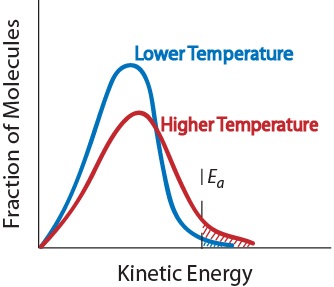
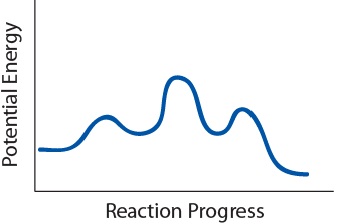
| activation energy (Ea) | The minimum amount of kinetic energy molecules must possess for an effective collision to occur | Factors that Affect the Rate of Reactions |
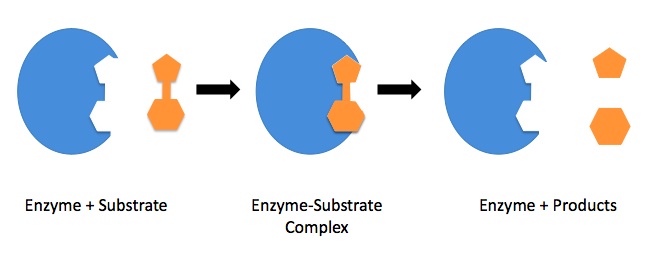
| active site | Area of enzymatic action where substrate molecules react | Catalysis |
| activity series | A list of elements that will replace elements below them in single-replacement reactions | Types of Chemical Reactions: Single- and Double-Displacement Reactions |
| actual yield | The amount that is actually produced in a chemical reaction | Yields |
| addition reaction | A reaction where atoms are added across a double or triple bond | Hydrocarbons |
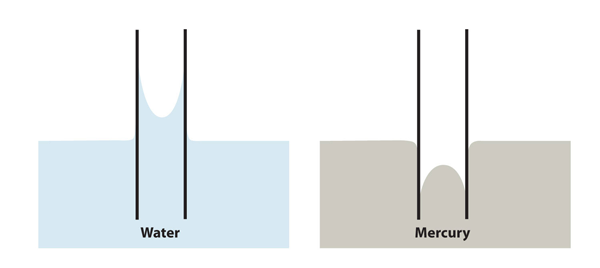
| adhesion | The tendency of a substance to interact with other substances because of intermolecular forces | Properties of Liquids |
| adsorb | Bind to the surface of another substance | Catalysis |
| alcohol | An organic compound that contains an OH functional group | Alkyl halides and alcohols |
| aldehyde | A compound that has a carbonyl functional group at the end of a chain of C atoms | Other Oxygen-Containing Functional Groups |
| aliphatic hydrocarbons | A hydrocarbon based on chains of C atoms | Hydrocarbons |
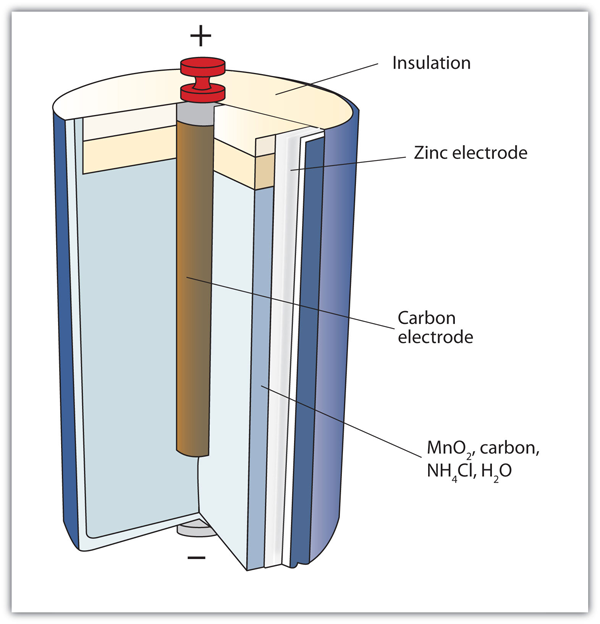
| alkaline battery | A type of dry cell that contains an alkaline (i.e., basic) moist paste, rather than an acidic paste | Applications of Redox Reactions: Voltaic Cells |
| alkane | An aliphatic hydrocarbon with only single covalent bonds | Hydrocarbons |
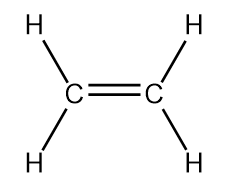
| alkene | An aliphatic hydrocarbon that contains a C–C double bond | Hydrocarbons |
| alkyl halide | An organic compound that contains a halogen atom | Alkyl halides and alcohols |
| alkyne | An aliphatic hydrocarbon that contains a C–C triple bond | Hydrocarbons |
| alpha particle | A type of radioactive emission equivalent to a helium nucleus | Radioactivity |
| amide group | A functional group that is the combination of the amine and carbonyl functional groups | Other Functional Groups |
| amide bond | The bond between the N atom and the C atom in an amide. | Other Functional Groups |
| amine | An organic derivative of ammonia | Other Functional Groups |
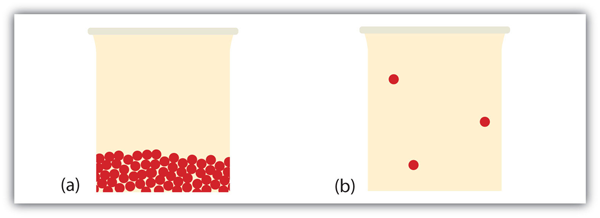
| amorphous solid | A solid with no long-term structure or repetition | Solids |
| amphiprotic | A substance that can act as a proton donor or a proton acceptor | Brønsted-Lowry Acids and Bases |
| analyte | The reagent of unknown concentration | Acid-Base Titrations |
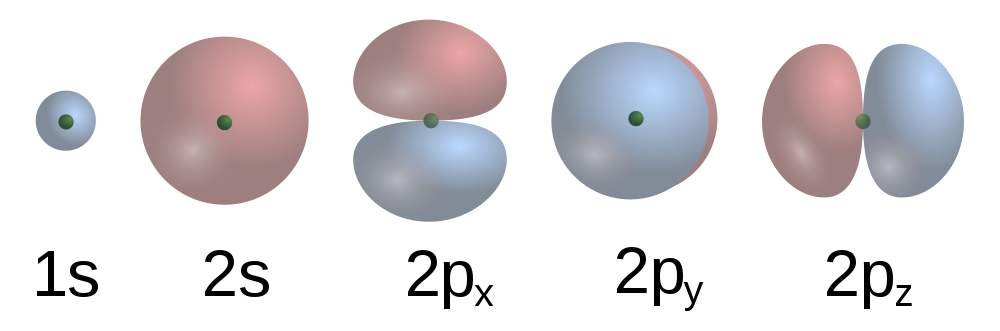
| angular momentum quantum number (ℓ) | An index that affects the energy and the spatial distribution of an electron in an atom. | Quantum Numbers for Electrons |
| anion | A species with an overall negative charge | Ions and Ionic Compounds |
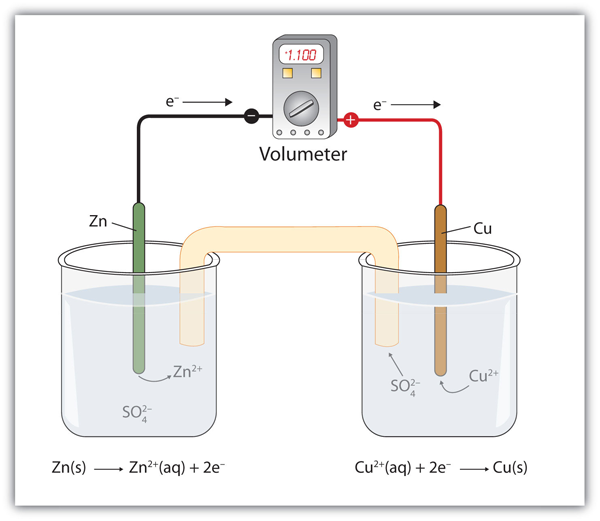
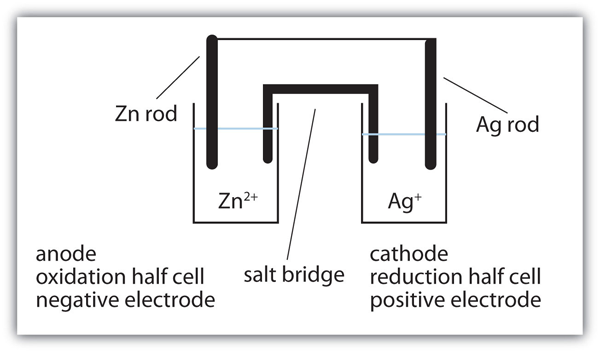
| anode | The half cell that contains the oxidation reaction | Applications of Redox Reactions: Voltaic Cells |
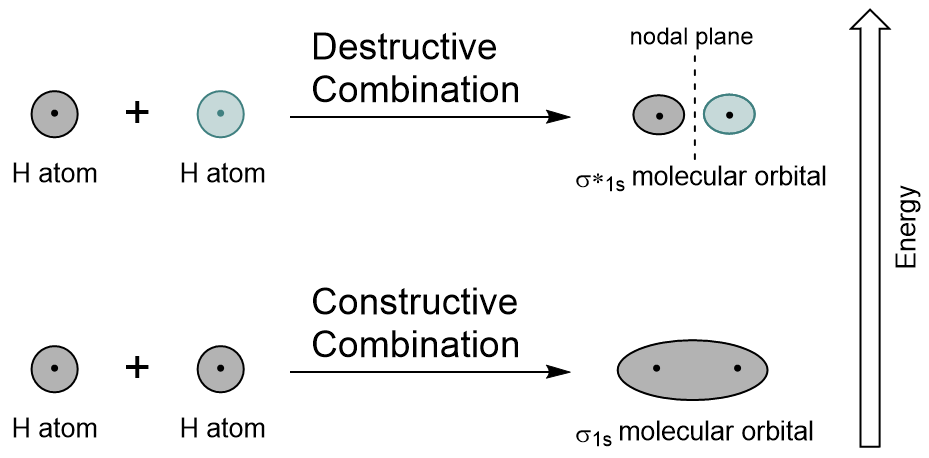
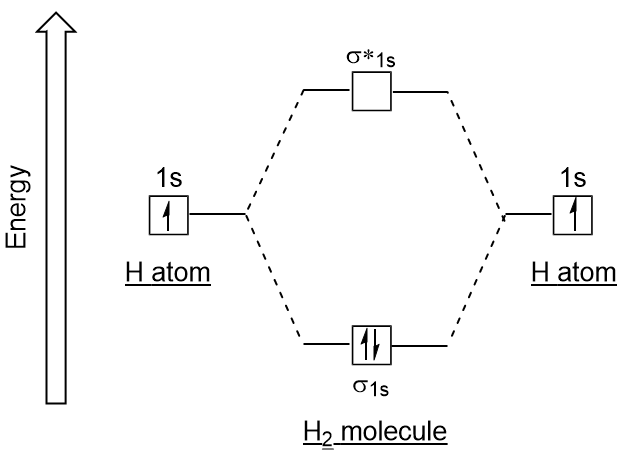
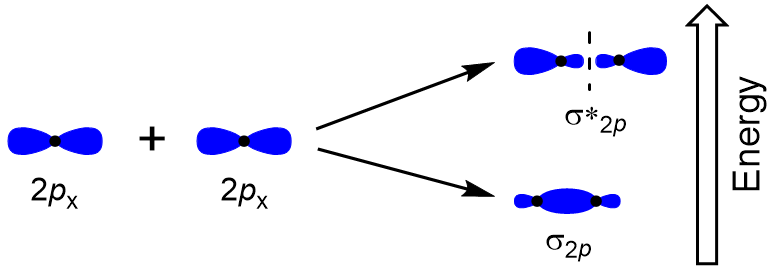
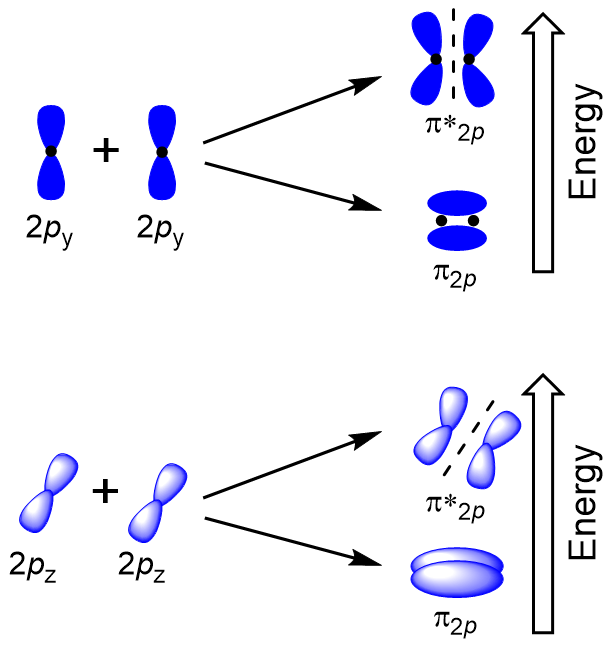
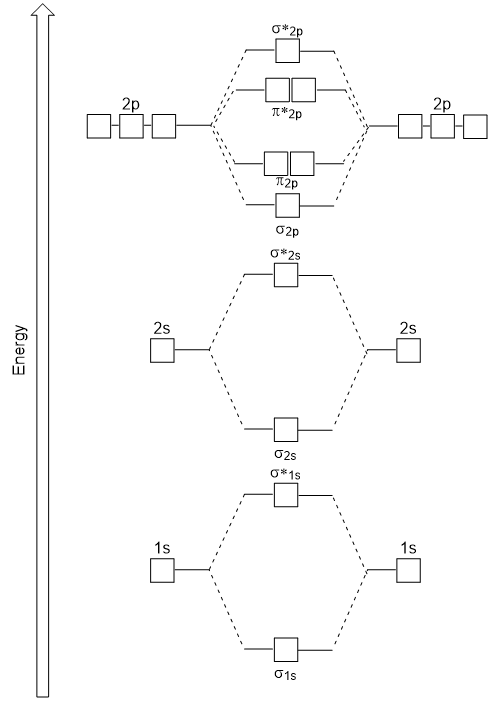
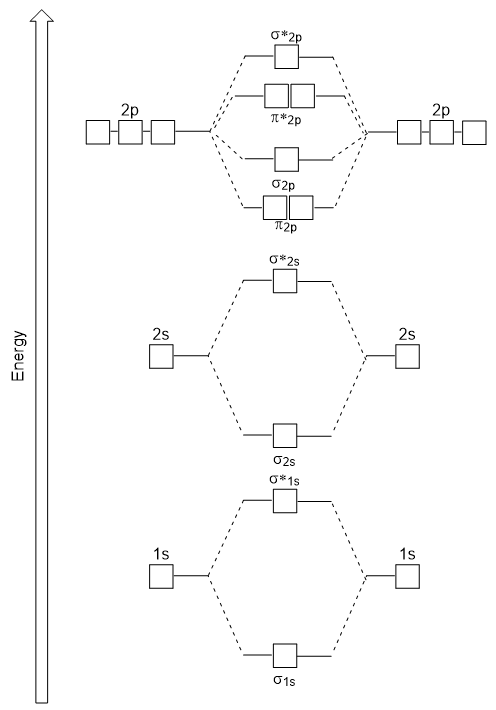
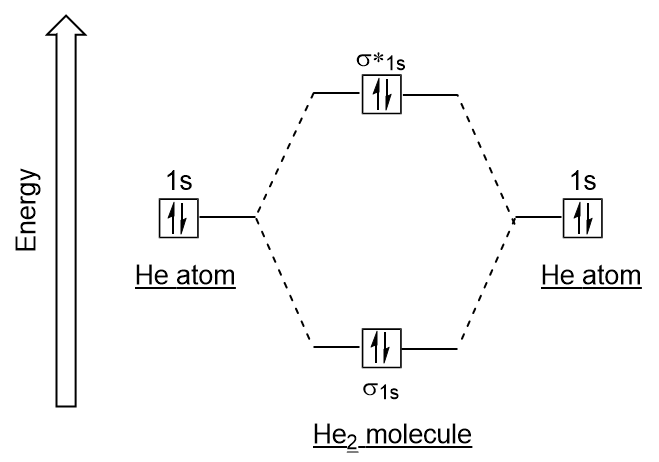
| antibonding molecular orbital | A higher energy molecular orbital generated by destructive combination of atomic orbitals | Molecular Orbitals |
| aromatic hydrocarbons | Flat ring systems, which contain continuously overlapping p orbitals, such as benzene | Hydrocarbons |
| Arrhenius acid | A compound that increases the hydrogen ion concentration in aqueous solution | Arrhenius Acids and Bases |
| Arrhenius base | A compound that increases the hydroxide ion concentration in aqueous solution | Arrhenius Acids and Bases |
| atmosphere (atm) | A unit of pressure equal to the average atmospheric pressure at sea level; defined as exactly 760 mmHg | Pressure |
| atom | The smallest piece of an element that maintains the identity of that element | Atomic Theory |
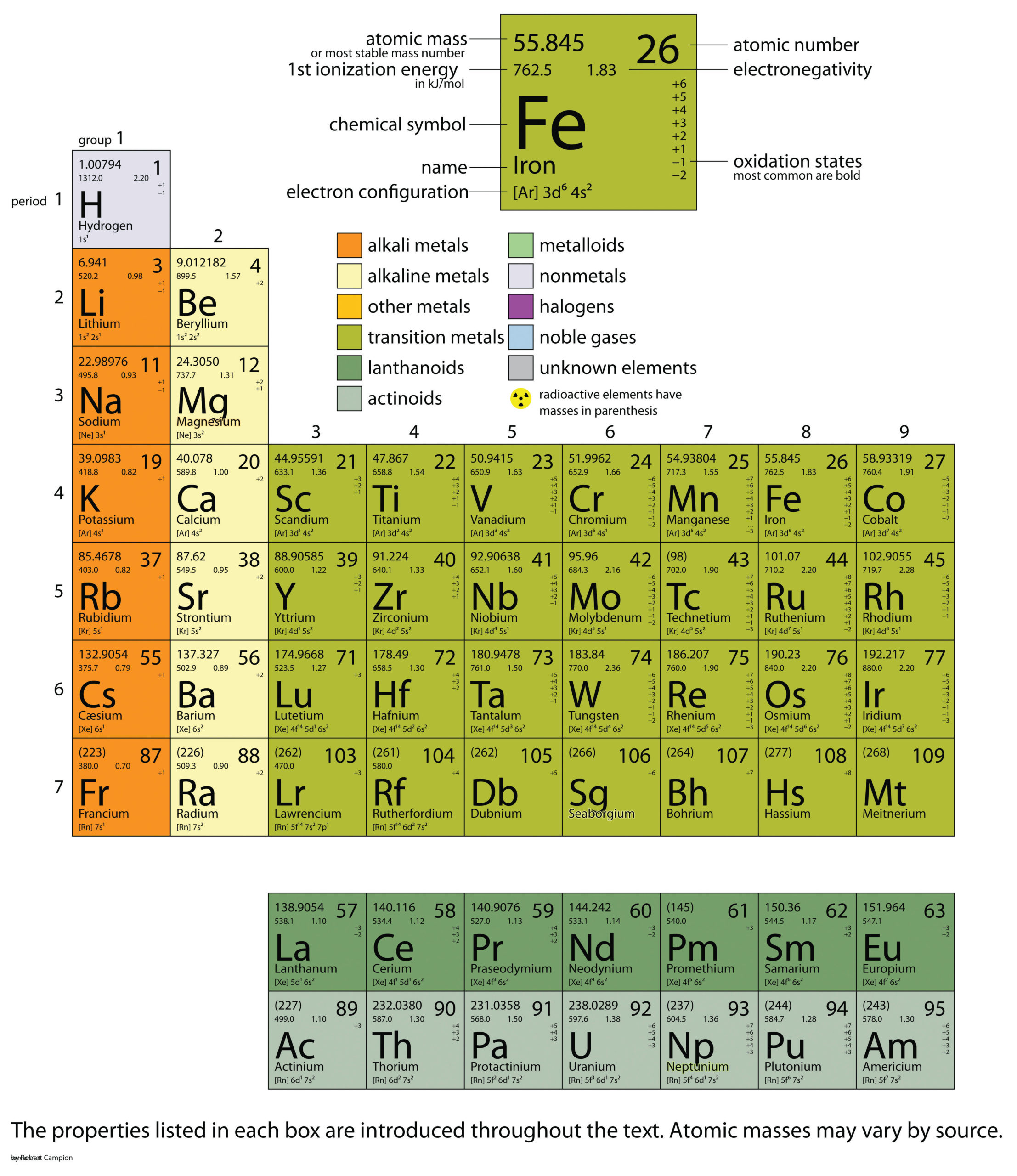
| atomic mass | The sum of the number of protons and neutrons in a nucleus | Atomic Theory |
| atomic mass | The weighted average of the masses of the isotopes that compose an element | Masses of Atoms and Molecules |
| atomic mass unit | One-twelfth of the mass of a carbon-12 atom | Masses of Atoms and Molecules |
| atomic number | The number of protons in an atom | Atomic Theory |
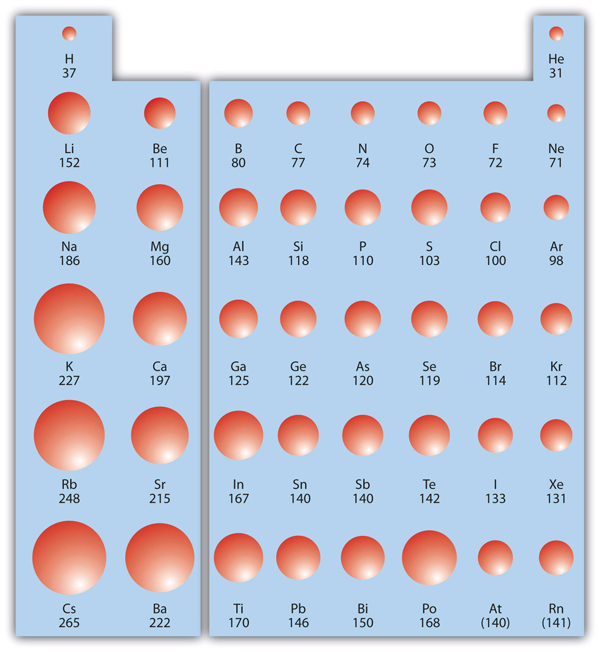
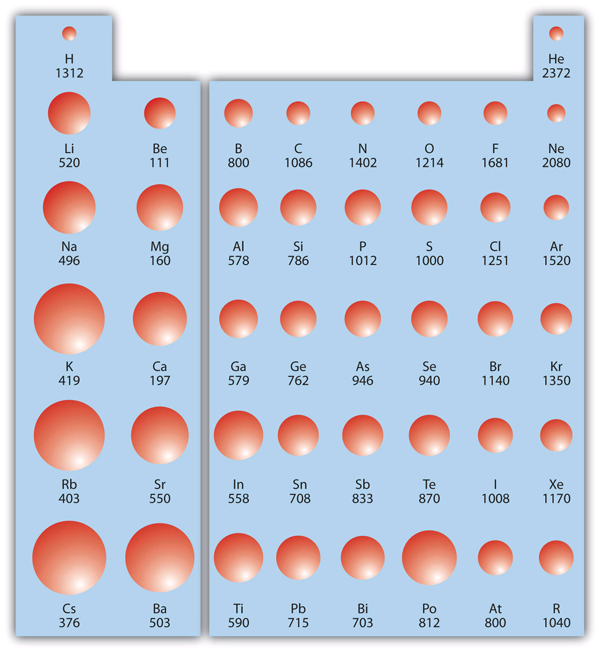
| atomic radius | An indication of the size of an atom. | Periodic Trends |
| atomic symbol | A one- or two-letter representation of the name of an element | Atomic Theory |
| atomic theory | The concept that atoms play a fundamental role in chemistry | Atomic Theory |
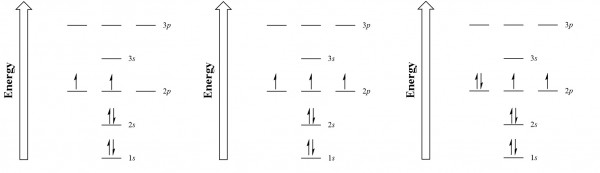
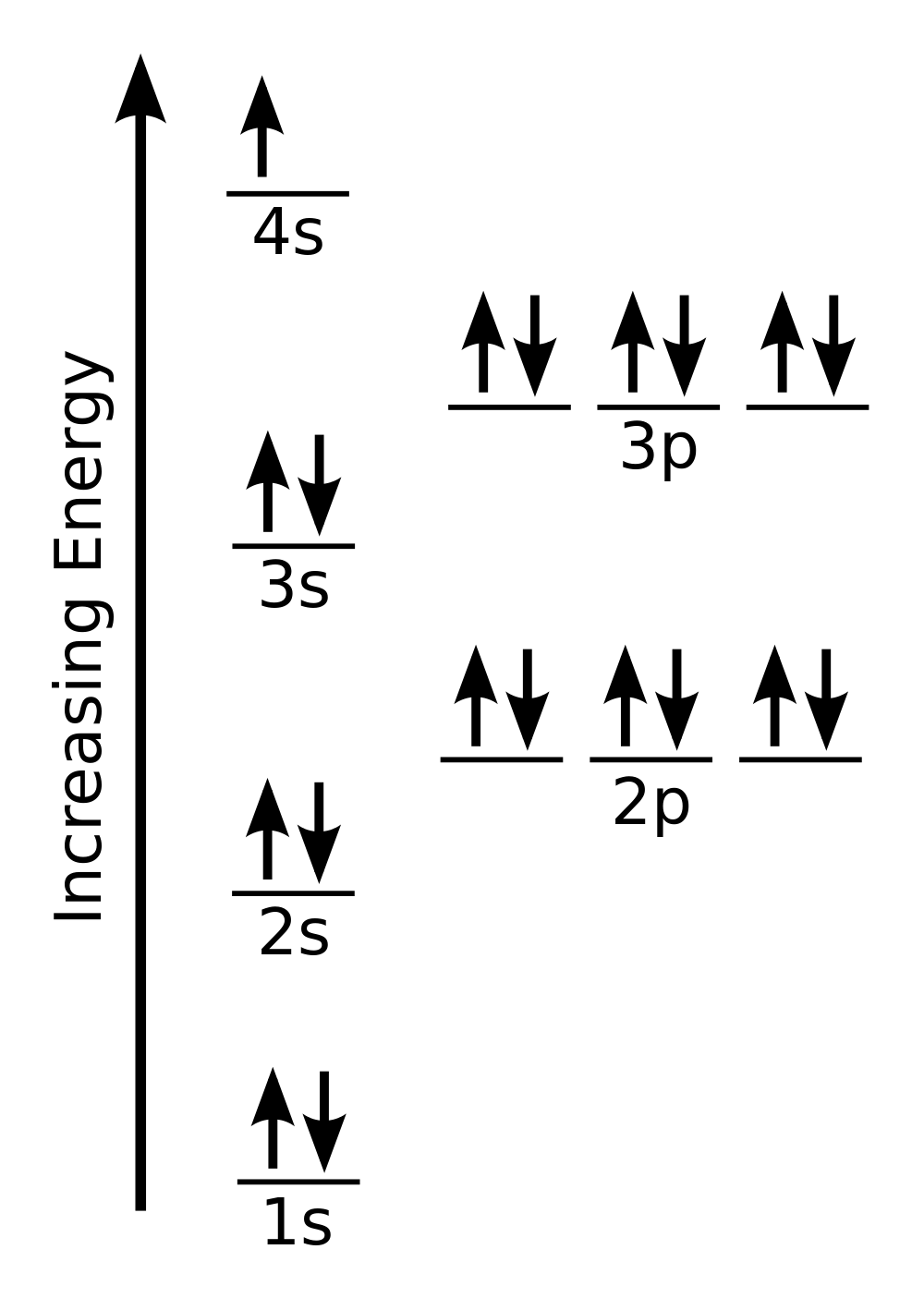
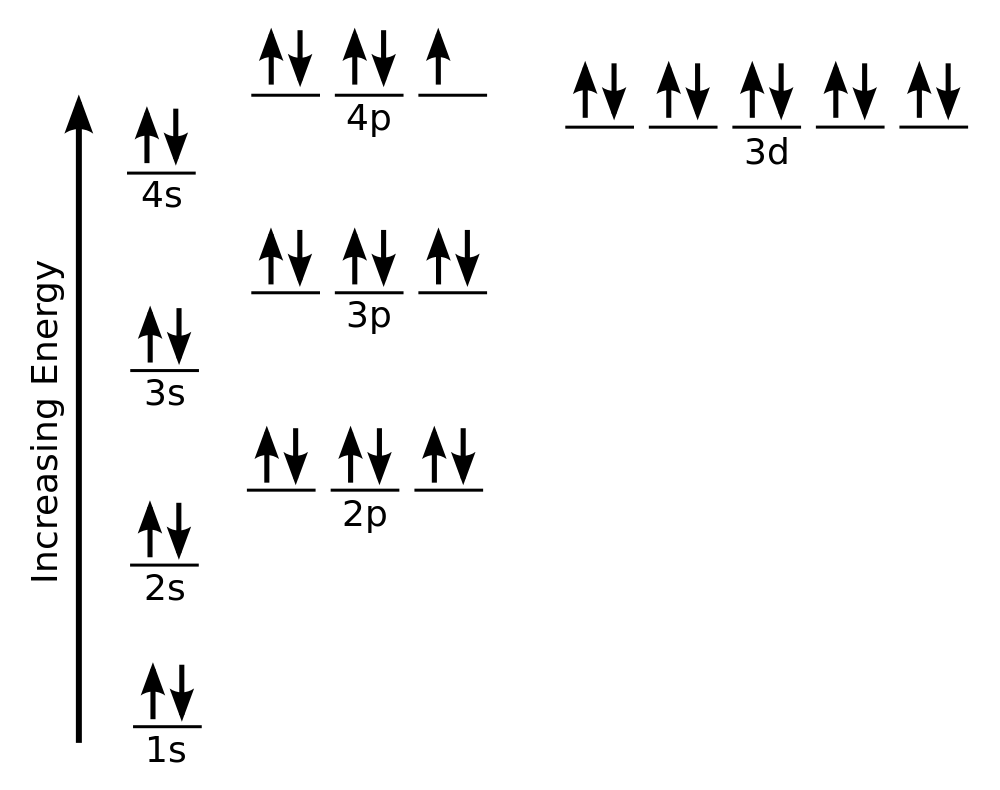
| aufbau principle | The way that electrons fill the lowest energy orbitals first. From the German for “building up.” | Organization of Electrons in Atoms |
| autoionization constant of water (Kw) | The product of the hydrogen ion and hydroxide ion concentrations | Autoionization of Water |
| autoionization of water | Water molecules act as acids (proton donors) and bases (proton acceptors) with each other to a tiny extent in all aqueous solutions | Autoionization of Water |
| Avogadro’s law | A gas law that relates number of particles to volume | Other Gas Laws |
| balanced chemical equation | A condition when the reactants and products of a chemical equation have the same number of atoms of all elements present | The Chemical Equation |
| base | A compound that increases the amount of OH− ions in an aqueous solution | Neutralization Reactions |
| basic salt | An ionic compound whose aqueous solution is slightly basic | Strong and Weak Acids and Bases and Their Salts |
| becquerel (Bq) | A unit of radioactivity equal to 1 decay per second | Units of Radioactivity |
| beta particle | A type of radioactive emission equivalent to an electron | Radioactivity |
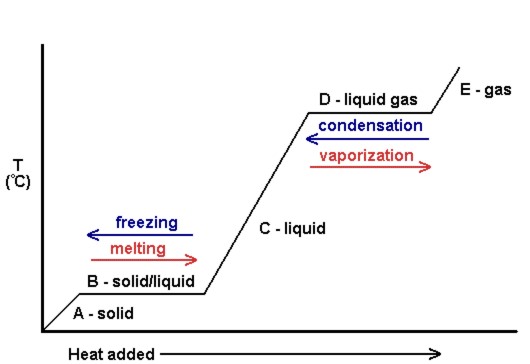
| boiling (or vaporization) | The process of a liquid becoming a gas | Phase Transitions: Melting, Boiling and Subliming |
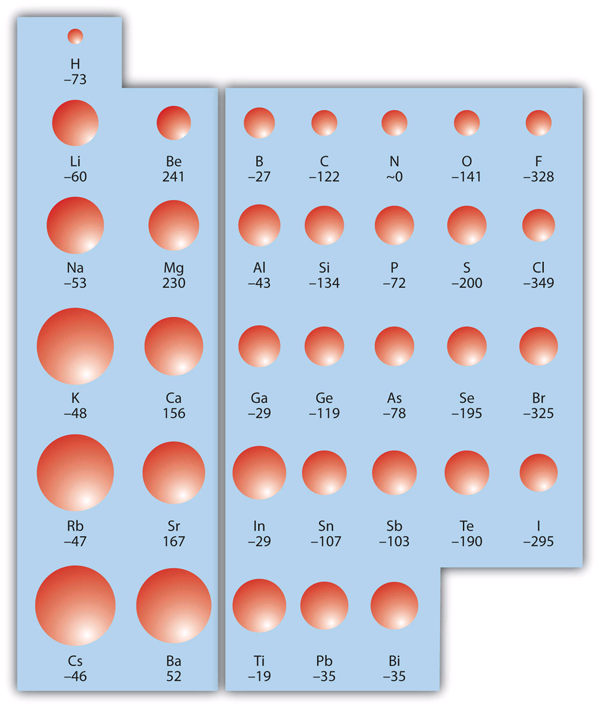
| boiling point | The characteristic temperature at which a liquid becomes a gas | Phase Transitions: Melting, Boiling and Subliming |
| boiling point elevation | The increase of a solution’s boiling point because of the presence of solute | Colligative Properties of Solutions |
| boiling point elevation constant (Kb) | The constant that relates the molality concentration of a solution and its boiling point change | Colligative Properties of Solutions |
| bond energy | The approximate amount of energy needed to break a covalent bond | Other Aspects of Covalent Bonding |
| bond order | A method of evaluating bond strength | Molecular Orbitals |
| bonding electron pair | A pair of electrons that makes a covalent bond | Covalent Bonds |
| bonding molecular orbital | The lower energy molecular orbital generated by constructive combination of atomic orbitals | Molecular Orbitals |
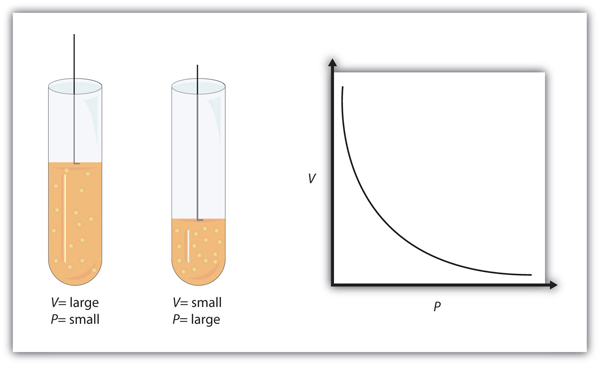
| Boyle’s law | A gas law that relates pressure and volume at constant temperature and amount | Gas Laws |
| branched hydrocarbons | A carbon compound that is not a straight chain, having substituents appended to the longest chain | Branched Hydrocarbons |
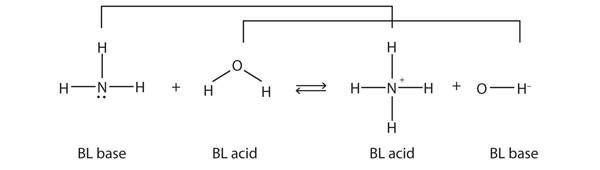
| Brønsted-Lowry acid | Any species that can donate a proton to another molecule | Brønsted-Lowry Acids and Bases |
| Brønsted-Lowry base | Any species that can accept a proton from another molecule | Brønsted-Lowry Acids and Bases |
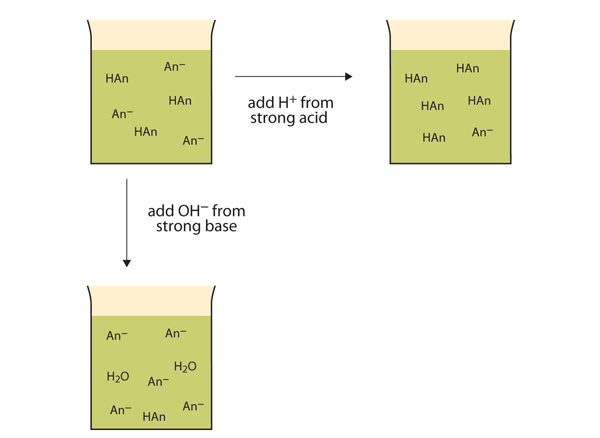
| buffer | A solution that resists dramatic changes in pH | Buffers |
| buffer capacity | The amount of strong acid or base a buffer can counteract | Buffers |
| burette or buret | A precisely calibrated volumetric delivery tube | Acid-Base Titrations |
| calorie | A unit of energy measurement originally defined in terms of warming up a given quantity of water. 1 cal = 4.184 J | Energy |
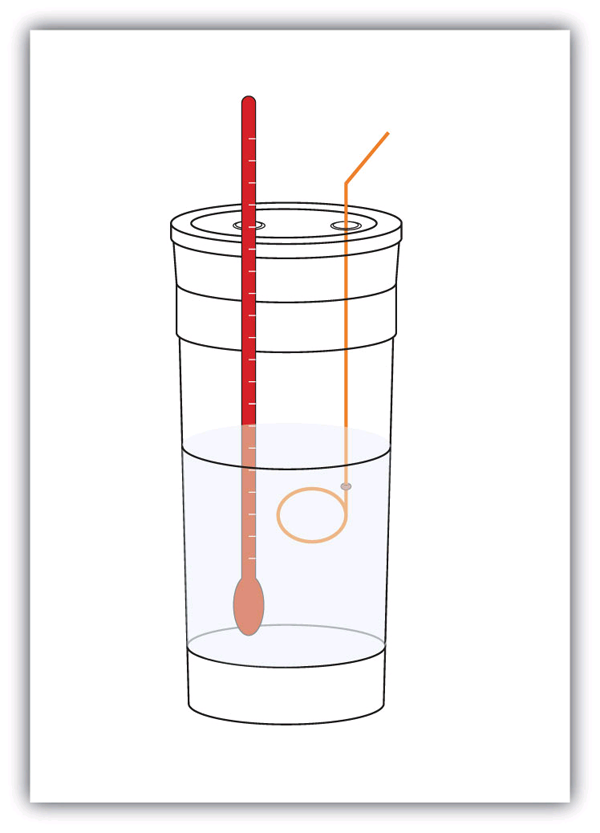
| calorimeter | A container used to measure the heat of a chemical reaction. | Enthalpy and Chemical Reactions |
| calorimetry | The process of measuring enthalpy changes in chemical reactions. | Enthalpy and Chemical Reactions |
| capillary action | The behavior of a liquid in narrow surfaces due to differences in adhesion and cohesion | Properties of Liquids |
| carbonyl group | A functional group where an O atom and a C atom are joined with a double bond | Other Oxygen-Containing Functional Groups |
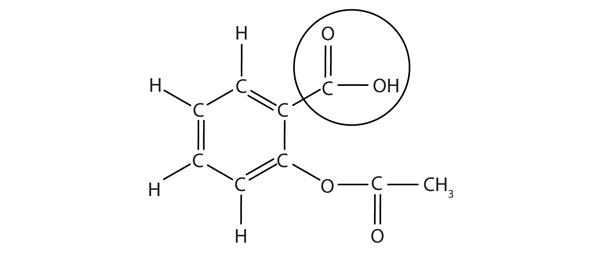
| carboxyl group | A functional group composed of a carbonyl group and an OH group | Other Oxygen-Containing Functional Groups |
| carboxylate ion | A negatively charged ion derived from a carboxylic acid | Other Oxygen-Containing Functional Groups |
| carboxylic acid | A molecule with a carboxyl group | Other Oxygen-Containing Functional Groups |
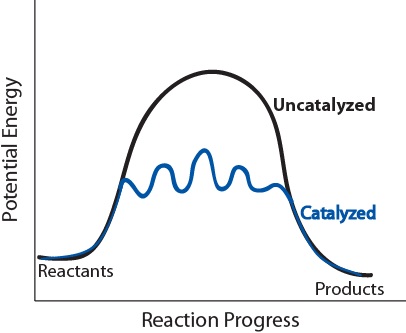
| catalyst | A substance that increases the speed of a reaction | Shifting Equilibria: Le Chatelier’s Principle |
| catalyst | A substance thaty accelerates a reaction by participating in it without being consumed | Factors that Affect the Rate of Reactions |
| catalyst | A substance that lowers the activation energy of a specific reaction by providing an alternate reaction pathway | Catalysis |
| cathode | The half cell that contains the reduction reaction | Applications of Redox Reactions: Voltaic Cells |
| cation | A species with an overall positive charge | Ions and Ionic Compounds |
| central atom | The atom in the center of a molecule | Covalent Bonds |
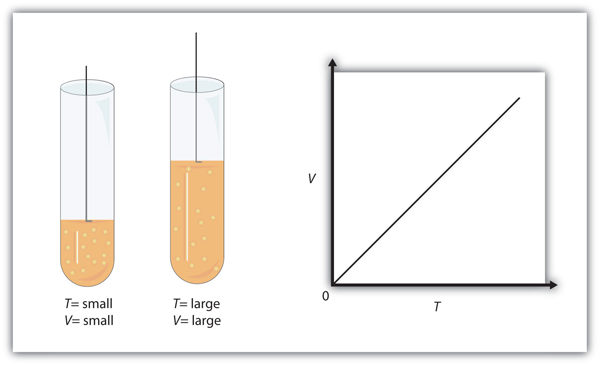
| Charles’s law | A gas law that relates volume and temperature at constant pressure and amount | Gas Laws |
| chemical bond | The connection between two atoms in a molecule | Molecules an Chemical Nomenclature |
| chemical change | The process of demonstrating a chemical property | Some Basic Definitions |
| chemical equation | A concise way of representing a chemical reaction | The Chemical Equation |
| chemical equilibrium | The point at which forward and reverse chemical reactions balance each other’s progress | Chemical Equilibrium |
| chemical nomenclature | A very specific system for naming compounds, in which unique substances get unique names | Molecules an Chemical Nomenclature |
| chemical property | A characteristic that describes how matter changes form in the presence of other matter | Some Basic Definitions |
| chemistry | The study of the interactions of matter with other matter and with energy | Introduction |
| coefficient | The part of a number in scientific notation that is multiplied by a power of 10 | Expressing Numbers |
| coefficient | A number in a chemical equation indicating more than one molecule of the substance | The Chemical Equation |
| cohesion | The tendency of a substance to interact with itself | Properties of Liquids |
| colligative property | A property of solutions related to the fraction that the solute particles occupy in the solution, not their identity | Colligative Properties of Solutions |
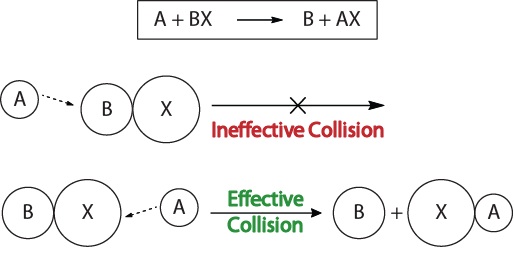
| collision theory | The theory that reactions occur when reactant molecules “effectively collide” | Factors that Affect the Rate of Reactions |
| combined gas law | A gas law that combines pressure, volume, and temperature | Other Gas Laws |
| combustion reaction | A chemical reaction in which a reactant combines with oxygen to produce oxides of all other elements as products | Composition, Decomposition, and Combustion Reactions |
| complete ionic equation | A chemical equation in which the dissolved ionic compounds are written as separated ions | Ionic Equations: A Closer Look |
| composition reaction | A chemical reaction in which a single substance is produced from multiple reactants | Composition, Decomposition, and Combustion Reactions |
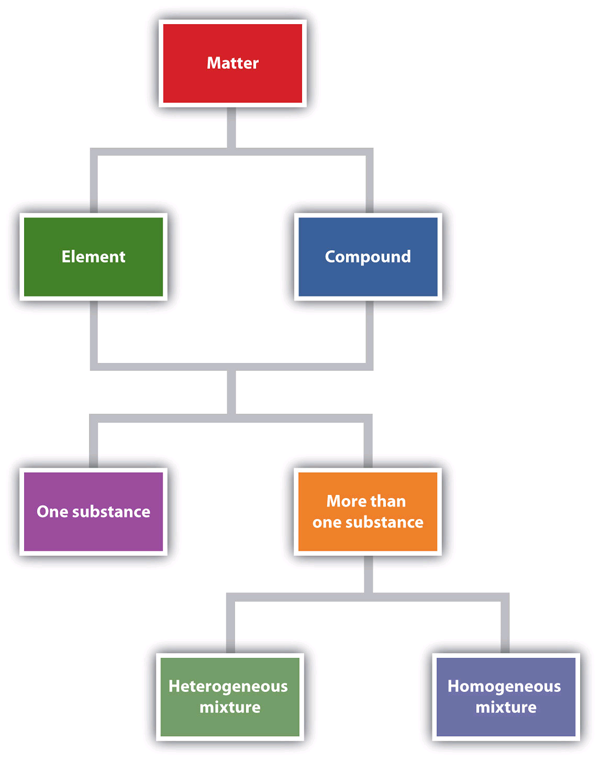
| compound | A combination of more than one element | Some Basic Definitions |
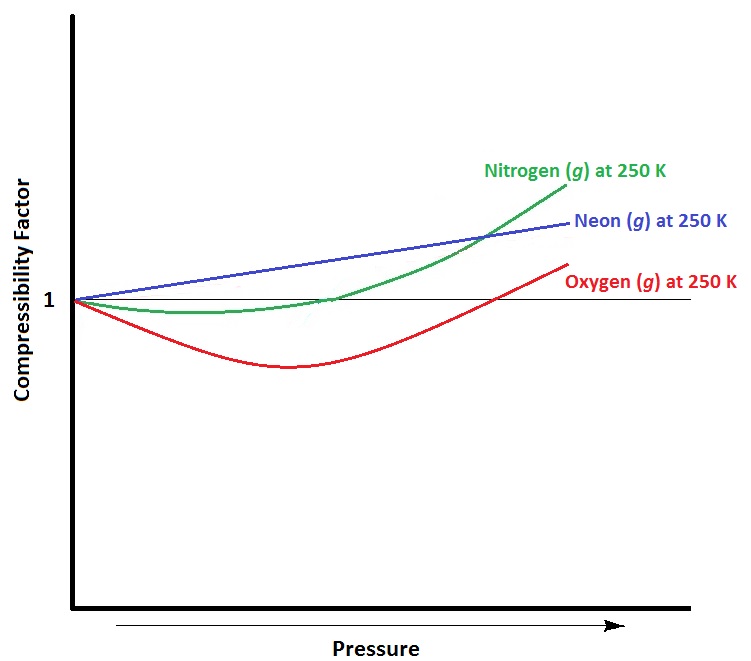
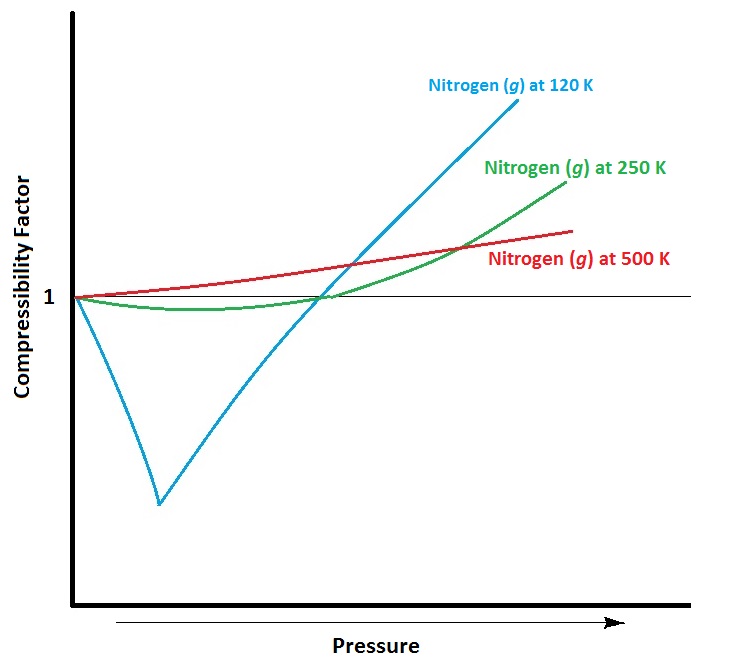
| compressibility factor | A measure of the extent of deviation from ideal gas behaviour. | Real Gases |
| concentrated solution | A solution with a lot of solute | Some Definitions |
| concentration | How much solute is dissolved in a given amount of solvent | Some Definitions |
| concentration (verb) | The removal of solvent, which increases the concentration of the solute in the solution | Dilutions and Concentrations |
| condensation | The process of a gas becoming a liquid | Phase Transitions: Melting, Boiling and Subliming |
| condensed structure | A listing of the atoms bonded to each C atom in a chain | Hydrocarbons |
| conjugate acid-base pair | Two species whose formulas differ by only a hydrogen ion | Brønsted-Lowry Acids and Bases |
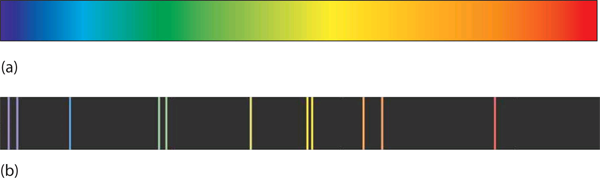
| continuous spectrum | An image that contains all colours of light. | Quantum Numbers for Electrons |
| conversion factor | A fraction that can be used to convert a quantity from one unit to another | Converting Units |
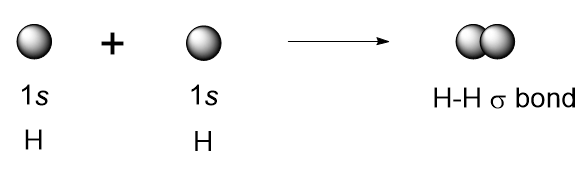
| covalent bond | A chemical bond formed by two atoms sharing electrons. | Covalent Bonds |
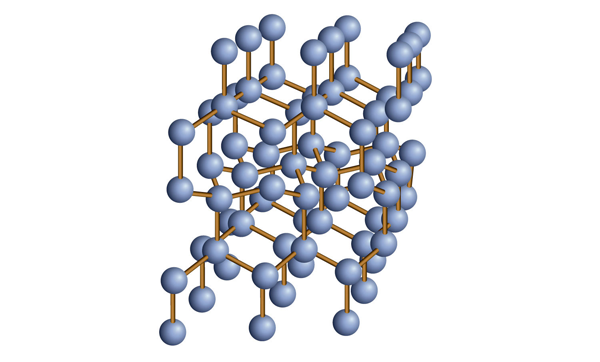
| covalent network solids | A crystalline solid composed of atoms of one or more elements that are covalently bonded together in a seemingly never-ending fashion | Solids |
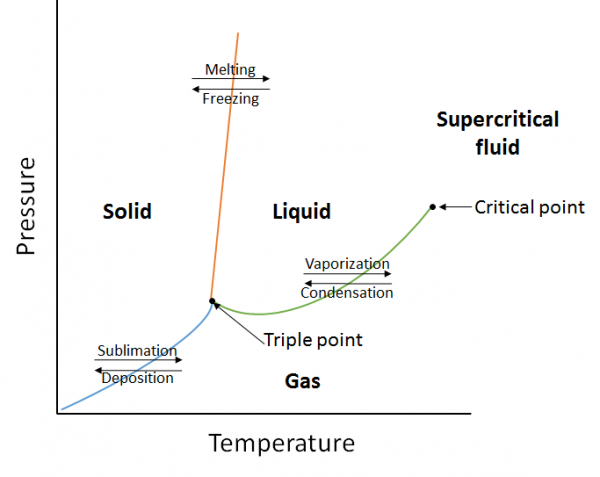
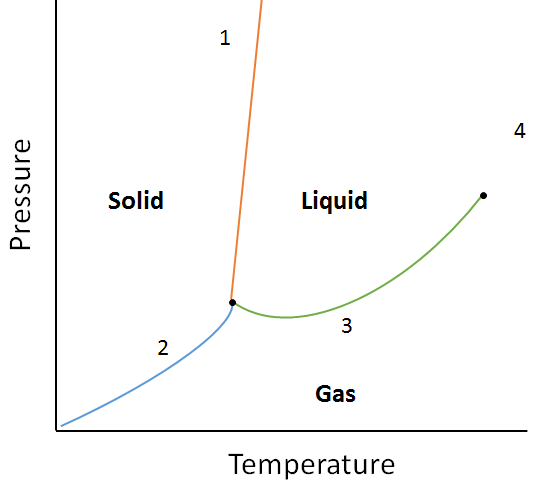
| critical point | The point at the highest temperature and pressure at which liquids and gases remain distinguishable | Properties of Liquids |
| crystalline solid | A solid with a regular, repeating three-dimensional structure | Solids |
| curie | A unit of radioactivity equal to 3.7×1010 decays/s | Units of Radioactivity |
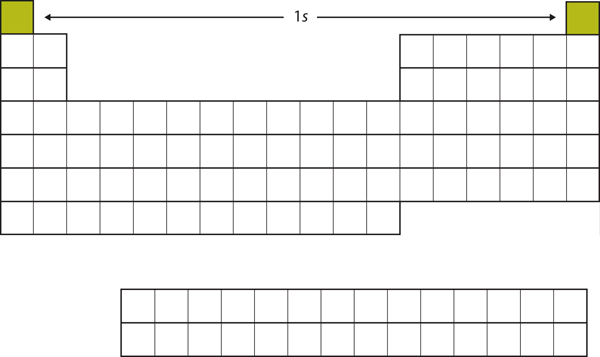
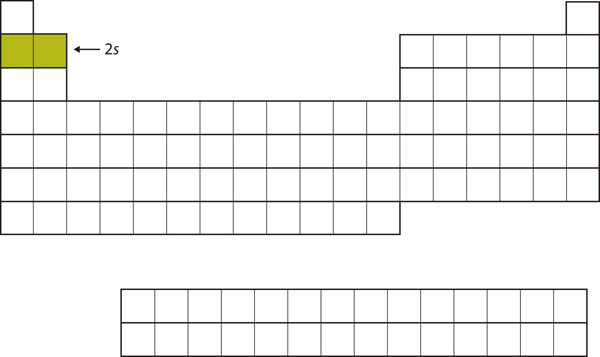
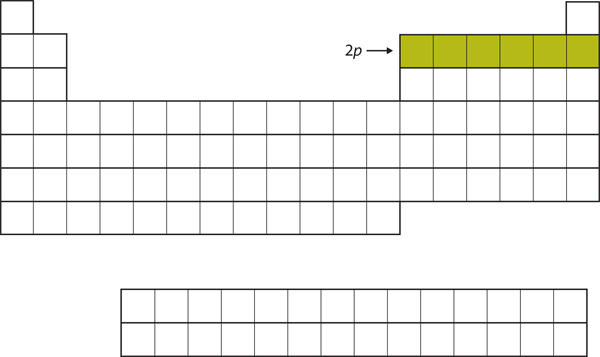
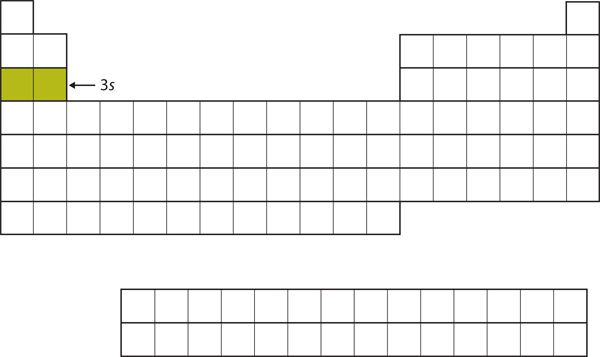
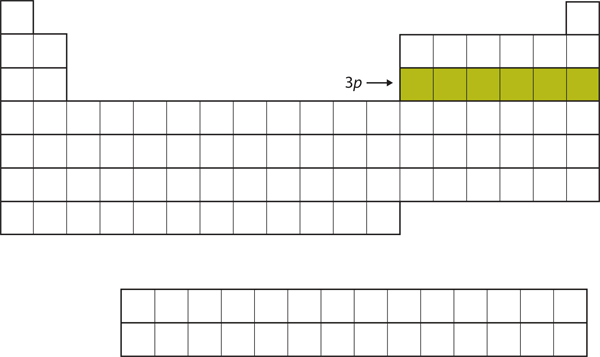
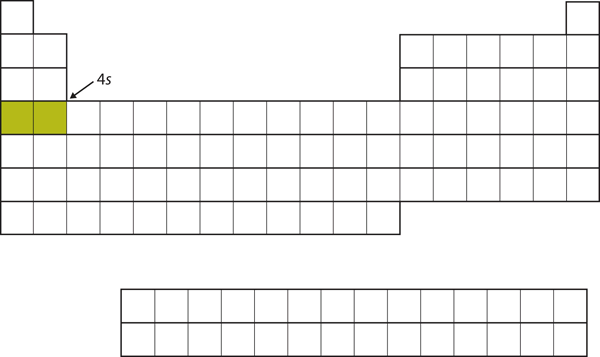
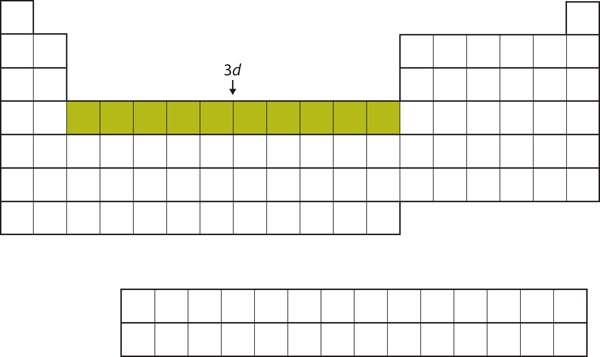
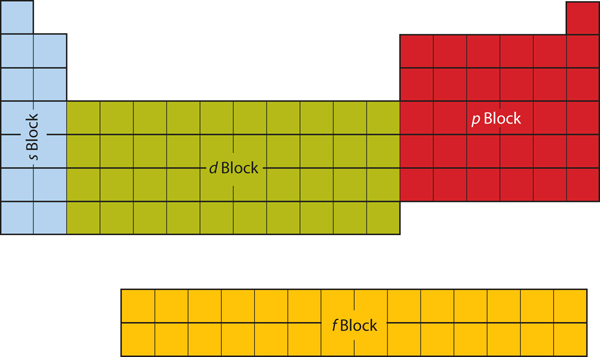
| d block | The columns of the periodic table in which d subshells are being occupied. | Electronic Structure and the Periodic Table |
| Dalton’s law of partial pressures | The total pressure of a gas mixture, Ptot, is equal to the sum of the partial pressures of the components, Pi | Gas Mixtures |
| daughter isotope | The product left over from the parent isotope in a nuclear equation | Radioactivity |
| decomposition reaction | A chemical reaction in which a single substance becomes more than one substance | Composition, Decomposition, and Combustion Reactions |
| degrees | The unit of temperature scales | Other Units: Temperature and Density |
| density | A physical property defined as a substance’s mass divided by its volume | Other Units: Temperature and Density |
| deposition | The process of a gas becoming a solid | Phase Transitions: Melting, Boiling and Subliming |
| derived unit | A unit that is a product or a quotient of a fundamental unit | Expressing Units |
| diatomic molecule | A molecule with only two atoms | Molecules an Chemical Nomenclature |
| diffusion | The movement of gas molecules through one or more additional types of gas via random molecular motion | Molecular Effusion and Diffusion |
| dilute | A solution with very little solute | Some Definitions |
| dilution | The addition of solvent, which decreases the concentration of the solute in the solution | Dilutions and Concentrations |
| dilution equation | The mathematical formula for calculating new concentrations or volumes when a solution is diluted or concentrated | Dilutions and Concentrations |
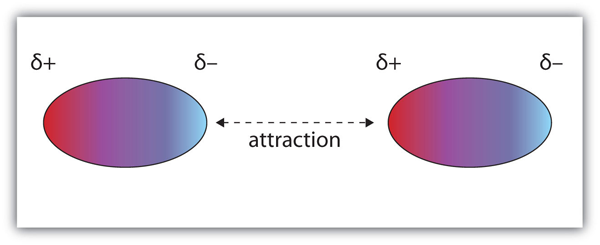
| dipole-dipole interactions | An intermolecular force caused by molecules with a permanent dipole | Intermolecular Forces |
| dispersion force (or London dispersion force) | An intermolecular force caused by the instantaneous position of an electron in a molecule | Intermolecular Forces |
| dissociation | The process of an ionic compound separating into ions when it dissolves | Ionic Equations: A Closer Look |
| double bond | A covalent bond composed of two pairs of bonding electrons | Covalent Bonds |
| double-replacement reaction | A chemical reaction in which parts of two ionic compounds are exchanged | Types of Chemical Reactions: Single- and Double-Displacement Reactions |
| dry cell | A modern battery that does not contain large amounts of aqueous solution | Applications of Redox Reactions: Voltaic Cells |
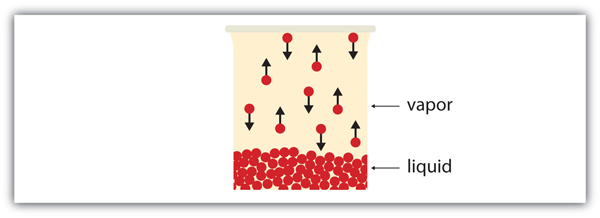
| dynamic equilibrium | When a process still occurs but the opposite process also occurs at the same rate so that there is no net change in the system. | Properties of Liquids |
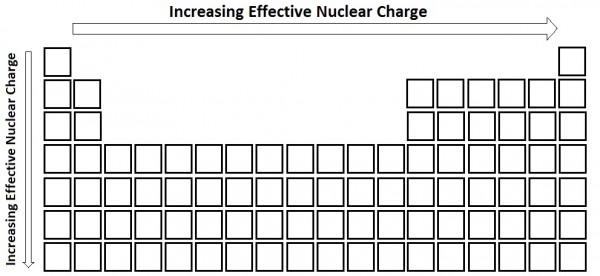
| effective nuclear charge (Zeff) | The net nuclear charge felt by valence electrons. | Periodic Trends |
| effusion | The movement of gas molecules from one container to another via a tiny hole | Molecular Effusion and Diffusion |
| electrodes | The cathode or anode of a voltaic cell | Applications of Redox Reactions: Voltaic Cells |
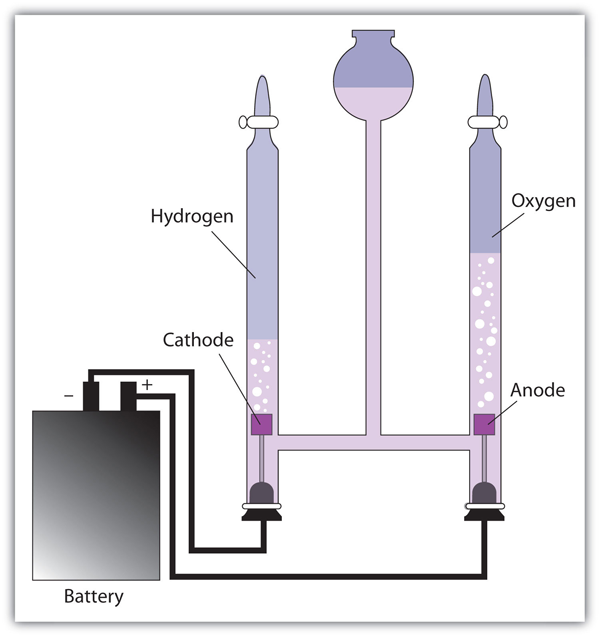
| electrolysis | The process of making a nonspontaneous redox reaction occur by forcing electricity into a cell | Electrolysis |
| electrolytic cell | A cell into which electricity is forced to make a nonspontaneous reaction occur | Electrolysis |
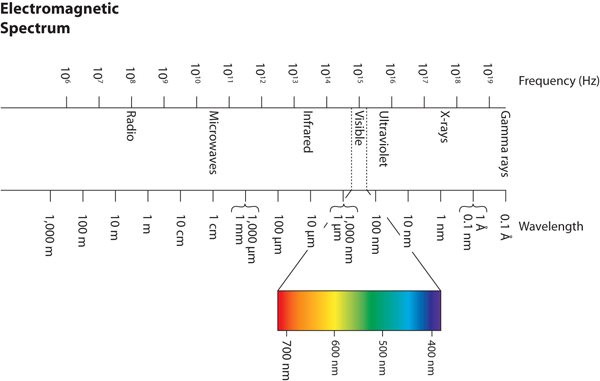
| electromagnetic spectrum | The full span of the possible wavelengths, frequencies, and energies of light. | Light |
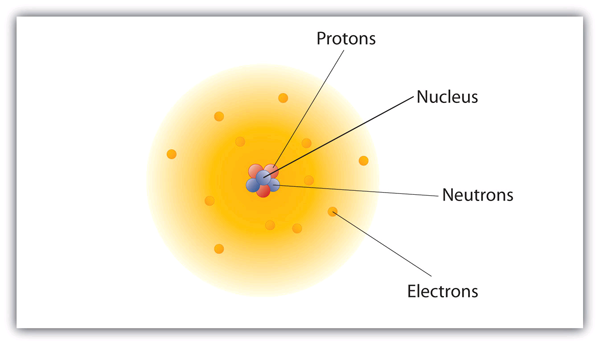
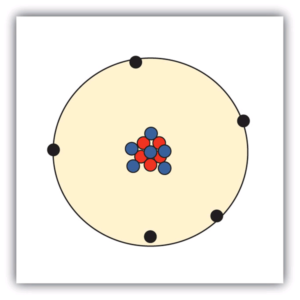
| electron | A tiny subatomic particle with a negative charge | Atomic Theory |
| electron affinity (EA) | The energy change when a gas-phase atom accepts an electron. | Periodic Trends |
| electron configuration | A listing of the shell and subshell labels. | Organization of Electrons in Atoms |
| electron deficient molecules | A molecule with less than eight electrons in the valence shell of an atom | Violations of the Octet Rule |
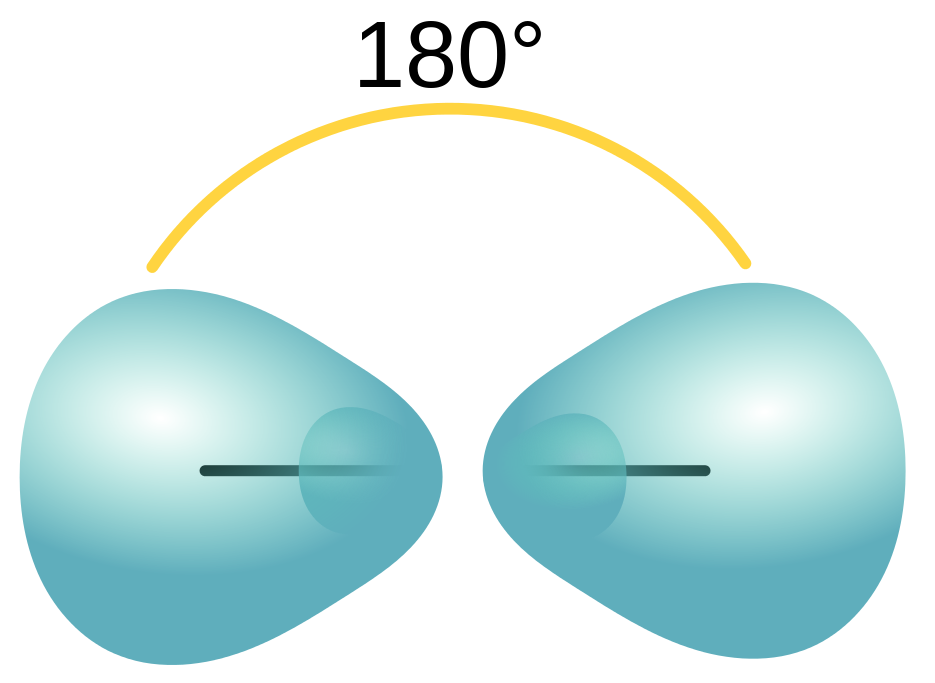
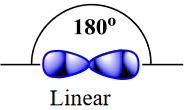
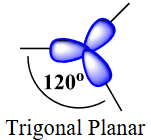
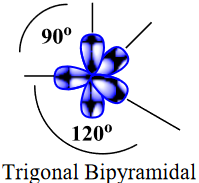
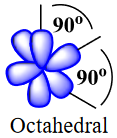
| electron group geometry | how electron groups (bonds and nonbonding electron pairs) are arranged | Molecular Shapes and Polarity |
| electron groups | A covalent bond of any type or a lone electron pair | Molecular Shapes and Polarity |
| electron shell | A term used to describe electrons with the same principal quantum number. | Quantum Numbers for Electrons |
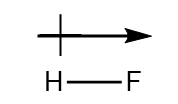
| electronegativity | A scale for judging how much atoms of any element attract electrons | Other Aspects of Covalent Bonding |
| electroplating | The deposition of a thin layer of metal on an object for protective or decorative purposes | Electrolysis |
| element | A substance that cannot be broken down into simpler chemical substances by ordinary chemical means | Some Basic Definitions |
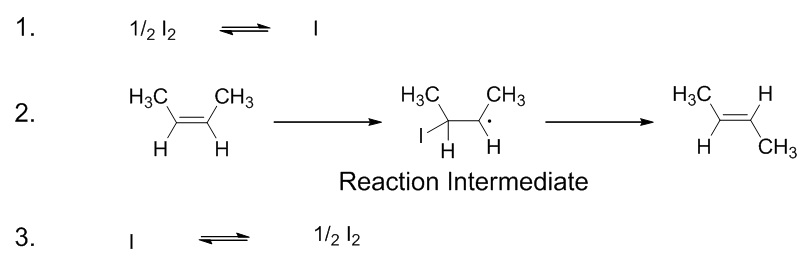
| elementary step | Each event that occurs in a chemical reaction as a result of an effective collision | Reaction Mechanisms |
| elimination reaction | The removal of a functional group (either X or OH) and a H atom from an adjacent carbon | Alkyl halides and alcohols |
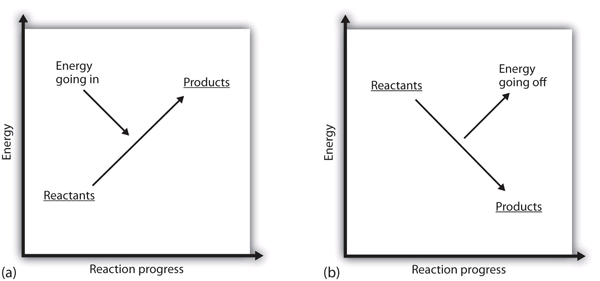
| endothermic | A chemical reaction that has a positive change in enthalpy. | Enthalpy and Chemical Reactions |
| energy | The ability to do work. | Energy |
| enthalpy change | The heat of a process at constant pressure. Denoted as ΔH. | Enthalpy and Chemical Reactions |
| enthalpy of formation | The enthalpy change for a formation reaction; denoted as ΔHf. | Formation Reactions |
| enthalpy of fusion | The amount of energy needed to change from a solid to a liquid or from a liquid to a solid | Phase Transitions: Melting, Boiling and Subliming |
| enthalpy of sublimation | The amount of energy needed to change from a solid to a gas or from a gas to a solid | Phase Transitions: Melting, Boiling and Subliming |
| enthalpy of vaporization | The amount of energy needed to change from a liquid to a gas or from a gas to a liquid | Phase Transitions: Melting, Boiling and Subliming |
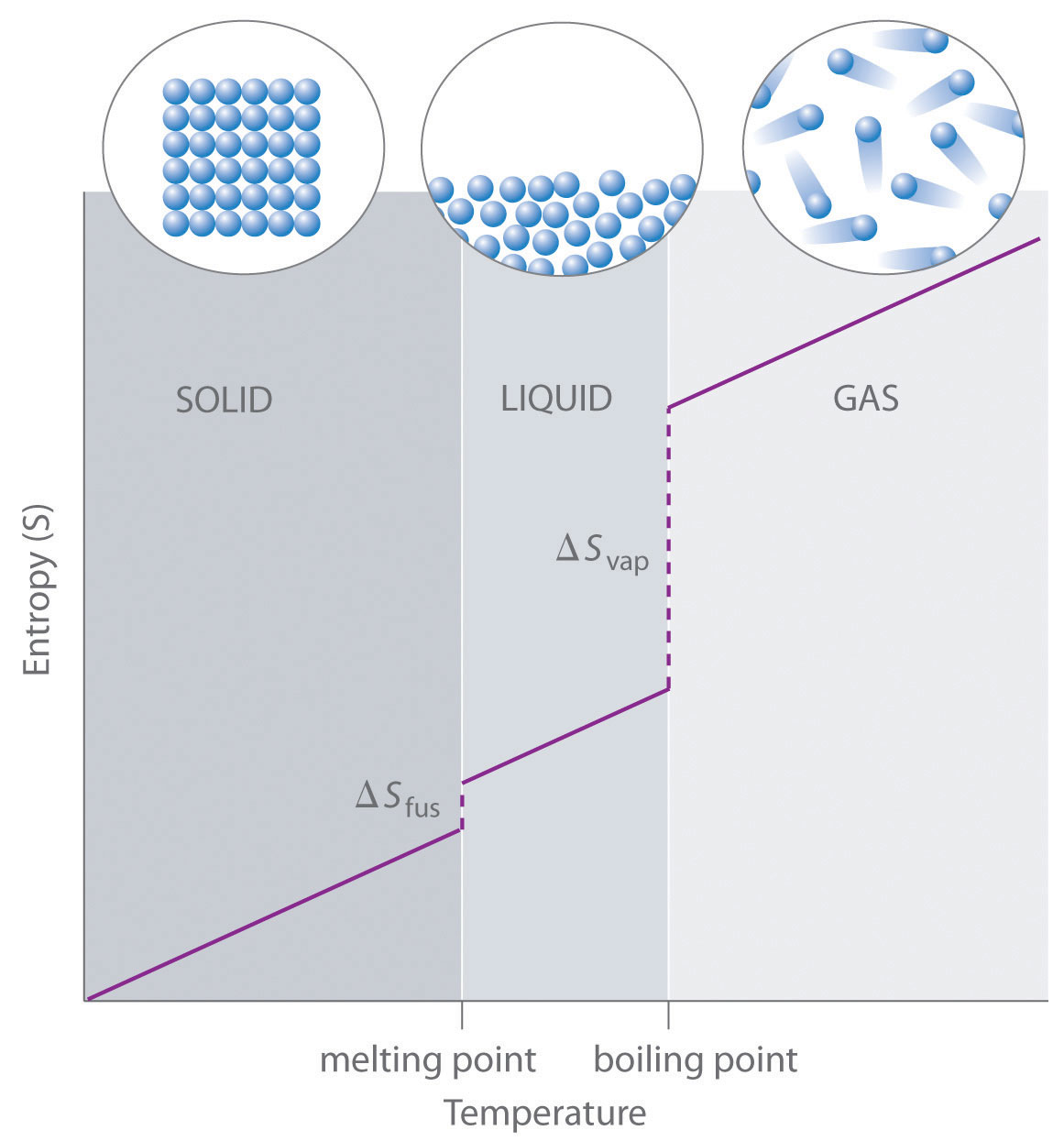
| entropy | The level of randomness (or disorder) of a system, or a measure of the energy dispersal of the molecules in the system | Entropy and the Second Law of Thermodynamics |
| enzyme | Protein molecules which serve to catalyze biochemical reactions | Catalysis |
| enzyme-substrate complex | The binding of substrate to the enzymatic active site | Catalysis |
| equilibrium constant (Keq) | A numerical value that relates to the ratio of products and reactants at equilibrium | The Equilibrium Constant |
| equivalence point | The point of the reaction when all the analyte has been reacted with the titrant | Acid-Base Titrations |
| ester group | A functional group made by combining a carboxylic acid with an alcohol | Other Oxygen-Containing Functional Groups |
| ether group | A functional group that has an O atom attached to two organic groups | Other Oxygen-Containing Functional Groups |
| evaporation | The formation of a gas phase from a liquid at temperatures below the boiling point | Properties of Liquids |
| exact number | A number from a defined relationship that technically has an infinite number of significant figures | Converting Units |
| exothermic | A chemical reaction that has a negative change in enthalpy. | Enthalpy and Chemical Reactions |
| expanded valence shell molecules | A molecule with more than eight electrons in the valence shell of an atom | Violations of the Octet Rule |
| experiment | A test of the natural universe to see if a guess (hypothesis) is correct | Chemistry as a Science |
| exponent | The raised number to the right of a 10 indicating the number of factors of 10 in the original number | Expressing Numbers |
| f block | The columns of the periodic table in which f subshells are being occupied. | Electronic Structure and the Periodic Table |
| fission | The breaking apart of an atomic nucleus into smaller nuclei | Radioactivity |
| formation reaction | A chemical reaction that forms one mole of a substance from its constituent elements in their standard states. | Formation Reactions |
| freezing point depression | The decrease of a solution’s freezing point because of the presence of solute | Colligative Properties of Solutions |
| freezing point depression constant (Kf) | The constant that relates the molality concentration of a solution and its freezing point change | Colligative Properties of Solutions |
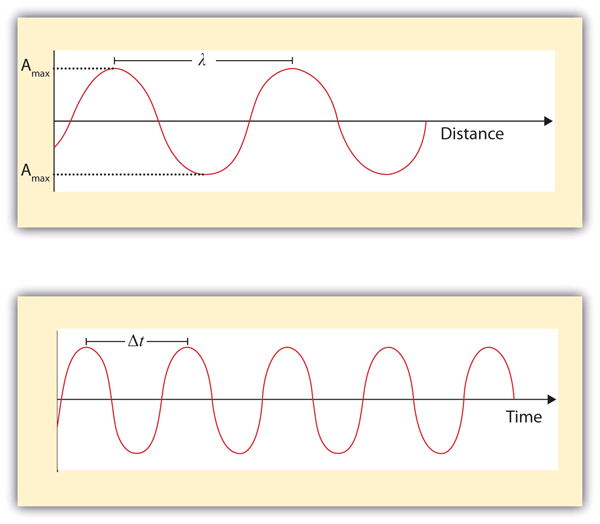
| frequency | The number of cycles of light that pass a given point in one second. | Light |
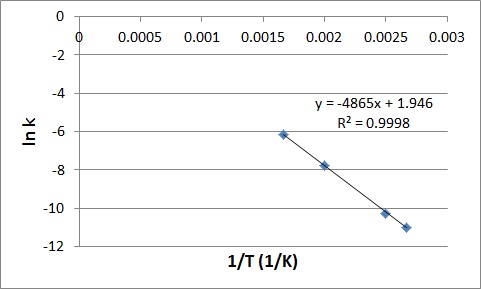
| frequency factor (A) | A factor that takes into account the frequency of reactions and the likelihood of correct molecular orientation | Activation Energy and the Arrhenius Equation |
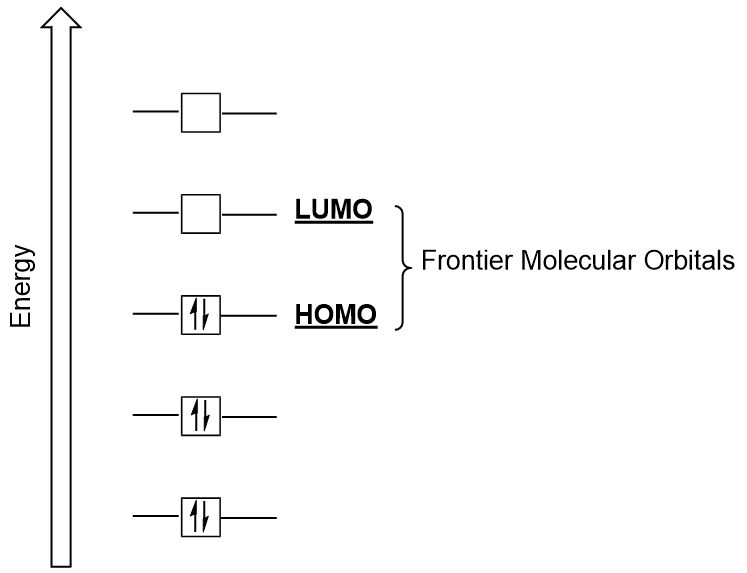
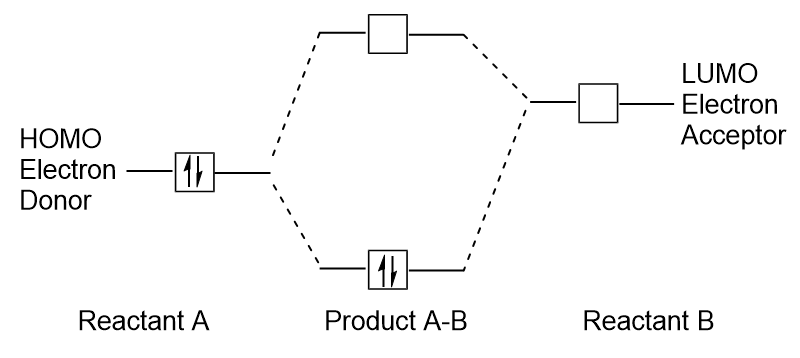
| frontier molecular orbitals | A term which refers to the HOMO and LUMO, the most likely orbitals to be involved in chemical reactions or processes | Molecular Orbitals |
| functional group | A collection of atoms or bonds with certain characteristic reactions | Alkyl halides and alcohols |
| fundamental units | One of the seven basic units of SI used in science | Expressing Units |
| gamma ray | A type of radioactive emission that is a very energetic form of electromagnetic radiation | Radioactivity |
| gas law | A simple mathematical formula that allows one to model, or predict, the behaviour of a gas | Gas Laws |
| Gay-Lussac’s law | A gas law that relates pressure with absolute temperature | Other Gas Laws |
| Geiger counter | An electrical device that detects radioactivity | Units of Radioactivity |
| Gibbs free energy (G) | A measure of spontaneity which incorporates both enthalpy and entropy | Gibbs Free Energy |
| Graham’s law of effusion | A law that relates the rate of effusion of a gas to the inverse of the square root of its molar mass. | Molecular Effusion and Diffusion |
| gray (Gy) | A unit of radioactive exposure equal to 100 rad | Units of Radioactivity |
| half cell | A part of a voltaic cell that contains one half reaction | Applications of Redox Reactions: Voltaic Cells |
| half reaction | The individual oxidation or reduction reaction of a redox reaction | Balancing Redox Reactions |
| half reaction method | The method of balancing redox reactions by writing and balancing the individual half reactions | Balancing Redox Reactions |
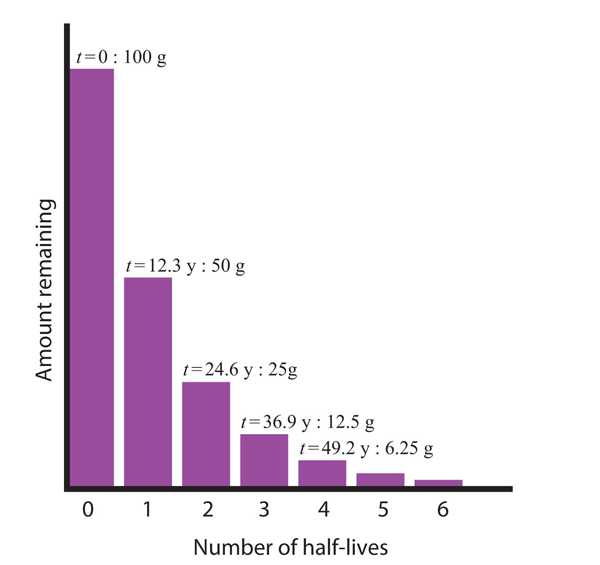
| half-life | The amount of time it takes for one-half of a radioactive isotope to decay | Half-Life |
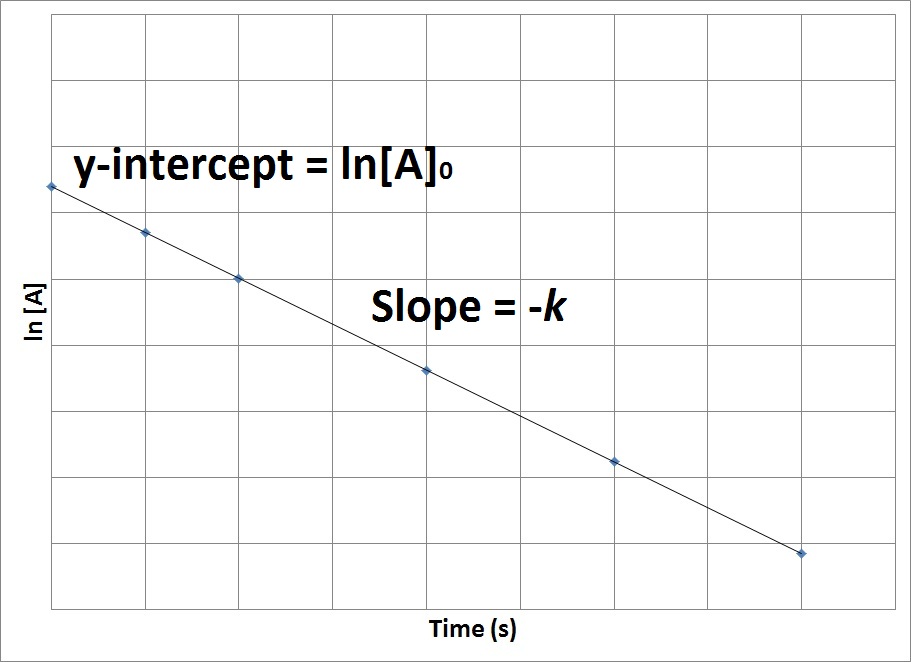
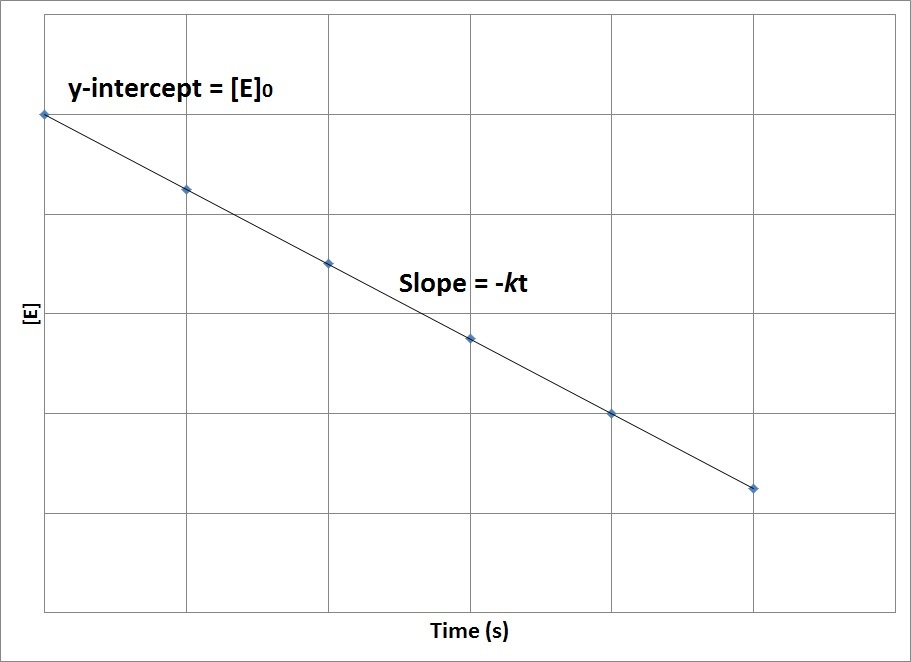
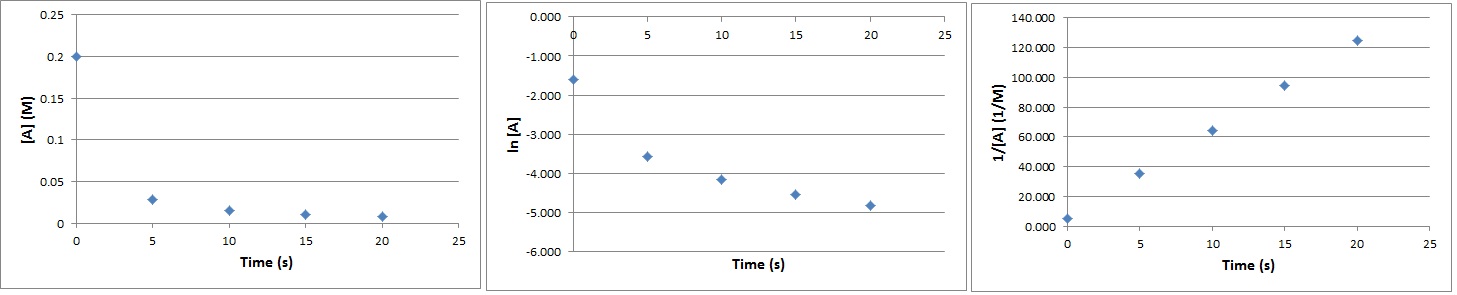
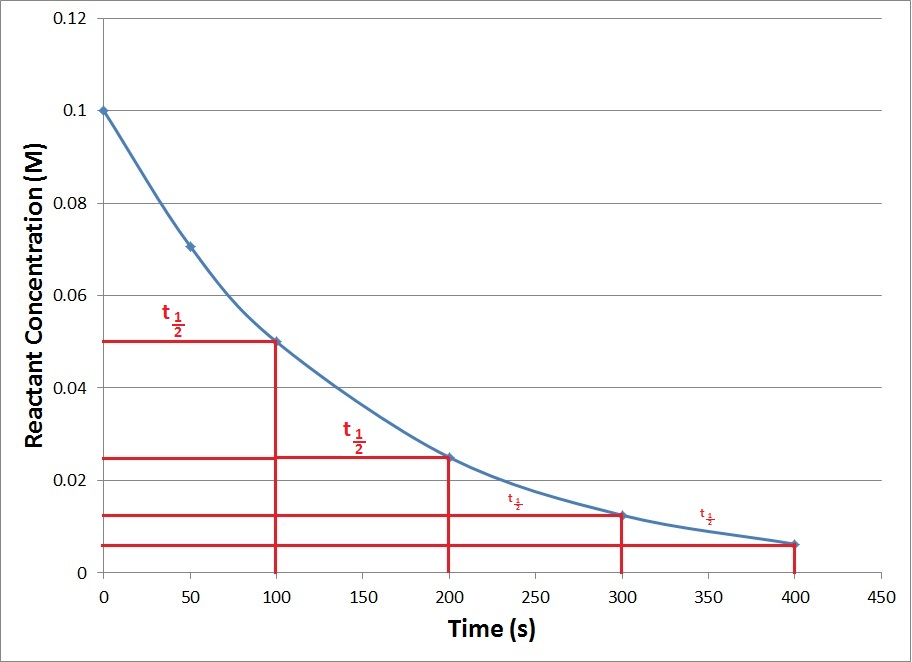
| half-life | The amount of time required for the concentration of a reactant to drop to one half of its initial concentration | Concentration-Time Relationships: Integrated Rate Laws |
| heat | The transfer of energy from one body to another due to a difference in temperature. | Work and Heat |
| heating curve | A plot of the temperature versus the amount of heat added | Phase Transitions: Melting, Boiling and Subliming |
| Hess’s law | When chemical equations are combined algebraically, their enthalpies can be combined in exactly the same way. | Hess’s Law |
| heterogeneous catalyst | A catalyst that is in a different phase from one or more of the reactants | Catalysis |
| heterogeneous equilibrium | An equilibrium in which more than one phase of reactants or products is present | The Equilibrium Constant |
| heterogeneous mixture | A non-uniform combination of more than one substance | Some Basic Definitions |
| HOMO | The highest occupied molecular orbital | Molecular Orbitals |
| homogeneous catalyst | A catalyst that is present in the same phase as the reactant molecules | Catalysis |
| homogeneous mixture | A uniform mixture of more than one substance that behaves as a single substance | Some Basic Definitions |
| Hund’s rule | One electron is placed in each degenerate orbital before pairing electrons in the same orbital. | Organization of Electrons in Atoms |
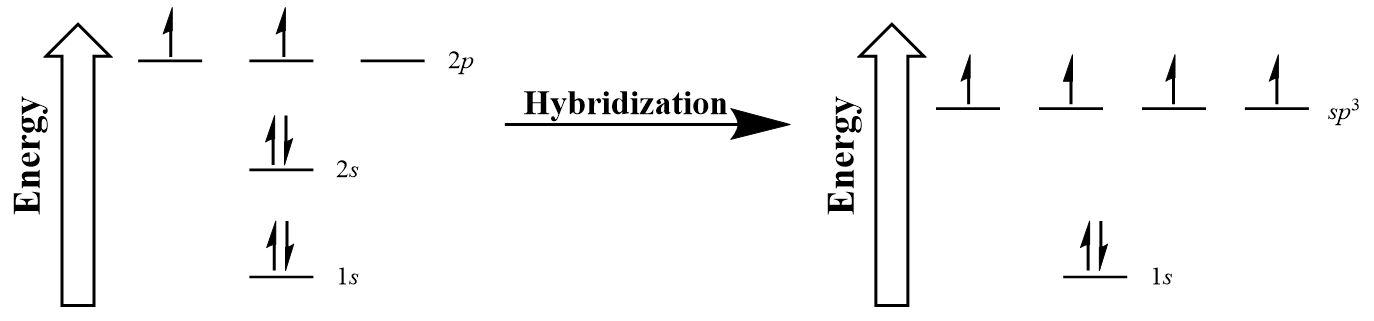
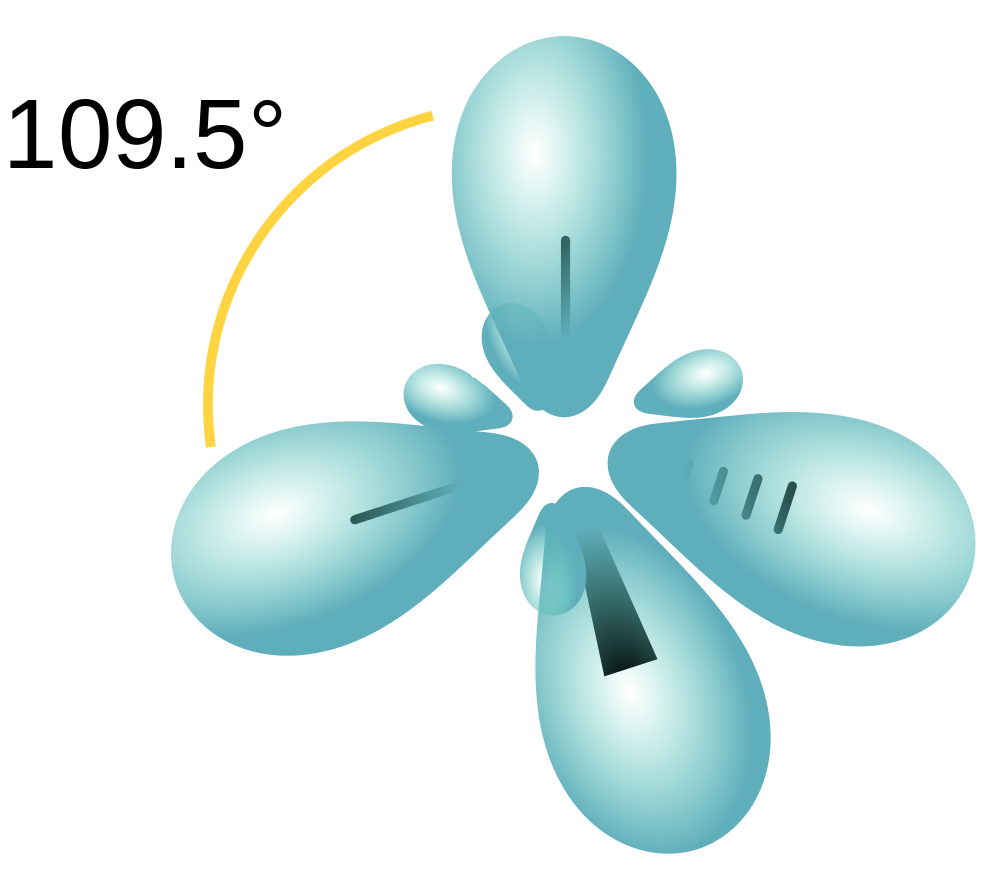
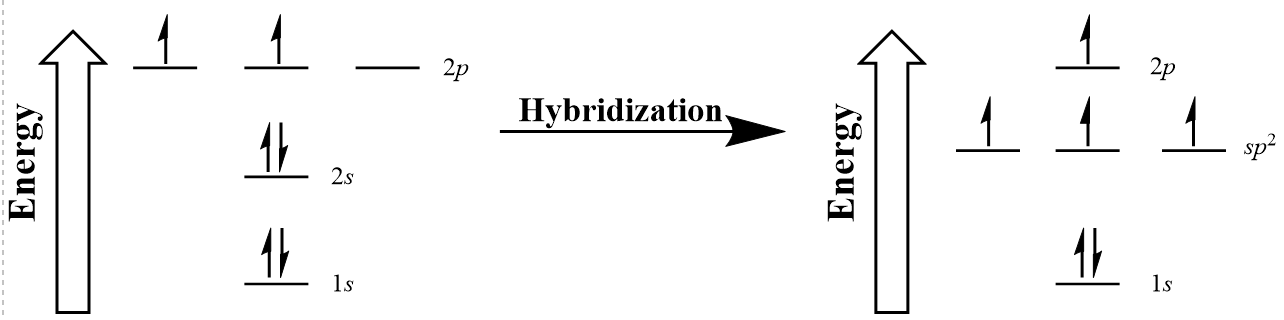
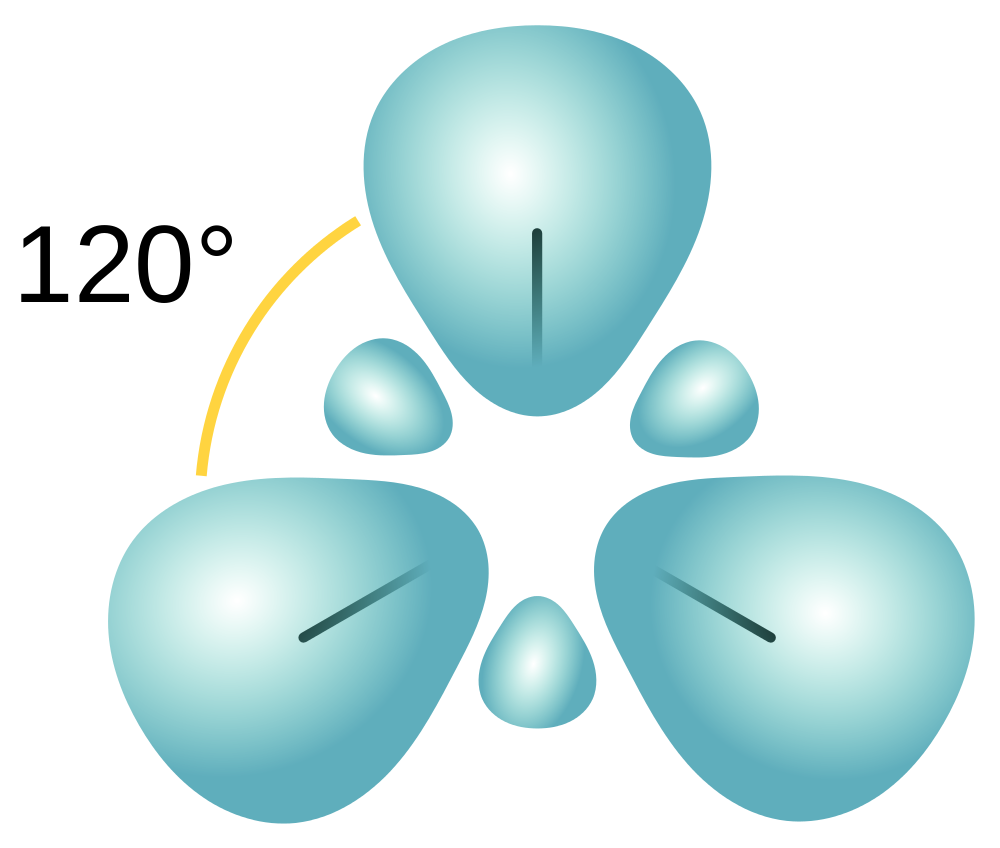
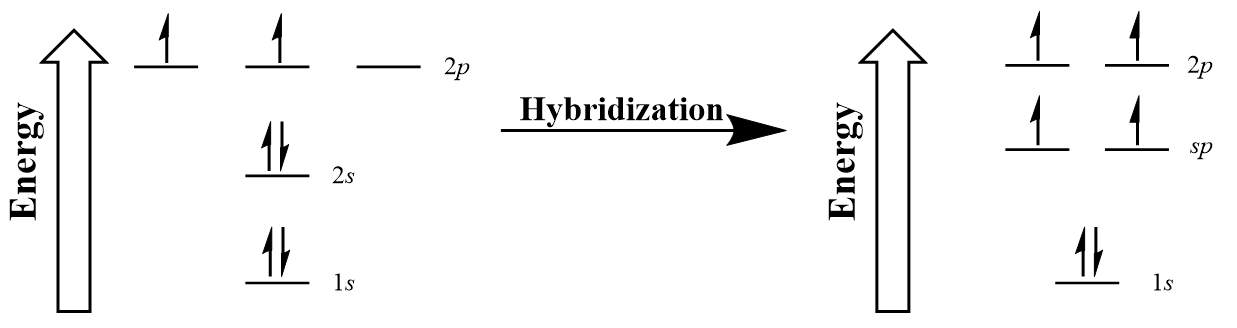
| hybridization | A mathematical mixing of atomic orbitals | Valence Bond Theory and Hybrid Orbitals |
| hydrocarbons | An organic compound composed of carbon and hydrogen | Hydrocarbons |
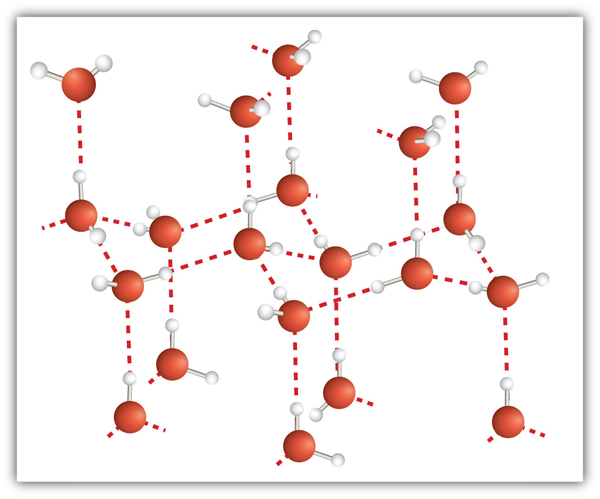
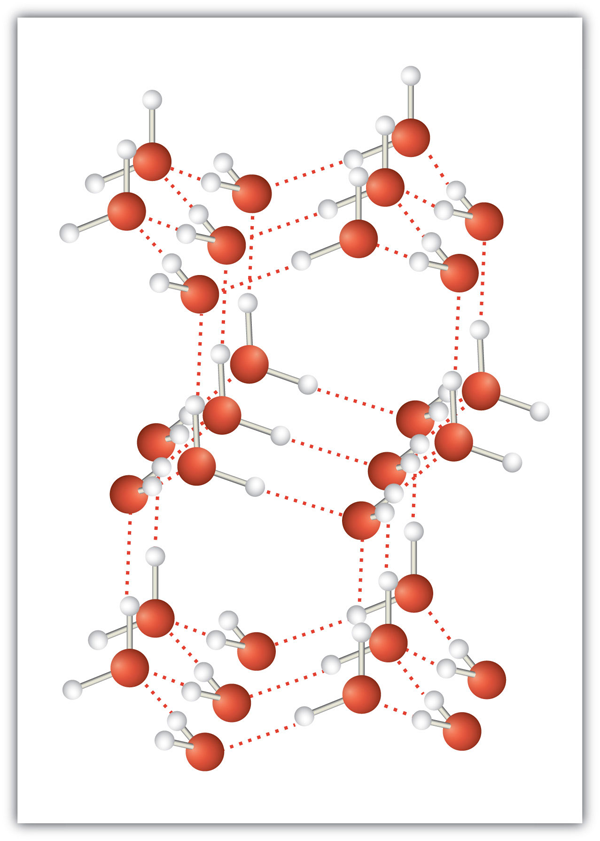
| hydrogen bonding | The very strong interaction between molecules due to H atoms being bonded to N, O, or F atoms | Intermolecular Forces |
| hydrogenation reaction | The reaction of hydrogen across a C–C double or triple bond, usually in the presence of a catalyst | Hydrocarbons |
| hydronium ion | The actual chemical species that represents a hydrogen ion in aqueous solution | Arrhenius Acids and Bases |
| hypothesis | An educated guess about how the natural universe works | Chemistry as a Science |
| hyrolysis | A reaction with water | Brønsted-Lowry Acids and Bases |
| ICE chart | A table used to calculate equilibria values featuring rows of initial, change and equlibria concentration | Calculating Equilibrium Constant Values |
| ideal gas | A gas that conforms exactly to the tenets of the kinetic molecular theory. | Real Gases |
| ideal gas law | A gas law that relates all four independent physical properties of a gas under any conditions | The Ideal Gas Law and Some Applications |
| indicator | A substance whose color change indicates the equivalence point of a titration | Acid-Base Titrations |
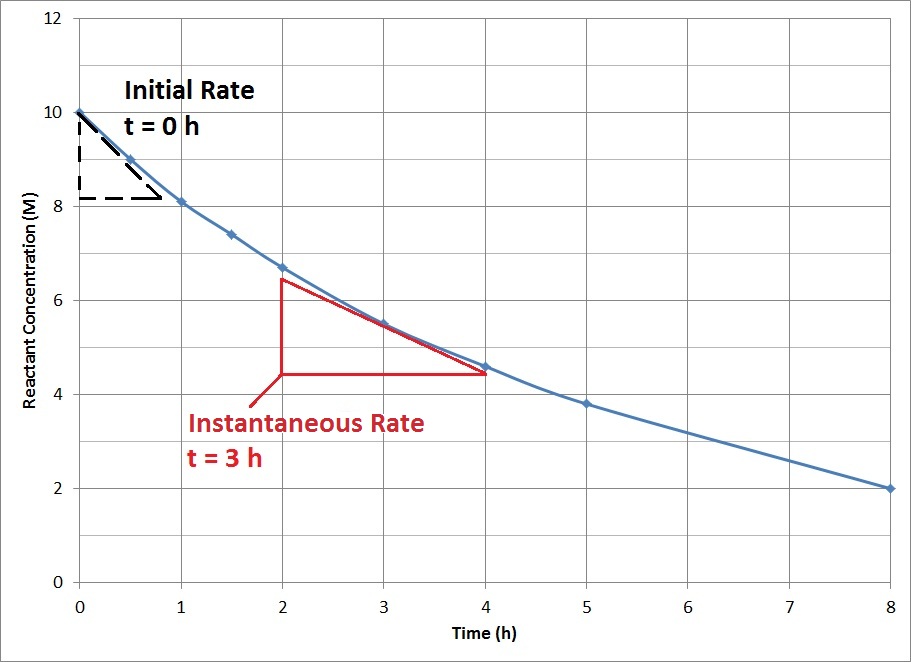
| initial rate | The instantaneous rate at the start of a reaction | Reaction Rates |
| initial rates method | A method to determine the rate law from the instantaneous reaction rate upon mixing the reactants | Rate Laws |
| instantaneous reaction rate | The rate of reaction at one instant in time | Reaction Rates |
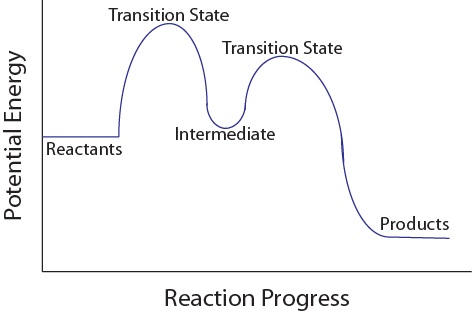
| intermediate | A chemical species does not appear in the overall balanced equation and is generated in one elementary step but used up in a subsequent step | Reaction Mechanisms |
| ion | A species with an overall electric charge | Ions and Ionic Compounds |
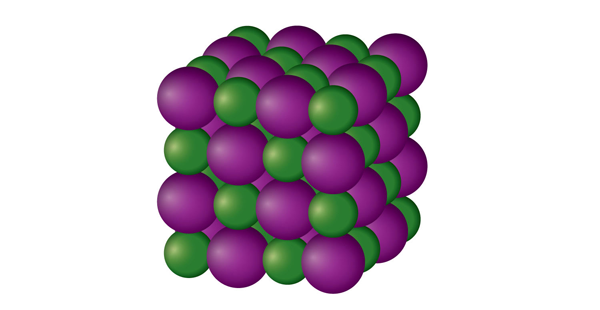
| ionic compound | A compound formed from positive and negative ions | Ions and Ionic Compounds |
| ionic formula | The chemical formula for an ionic compound | Ions and Ionic Compounds |
| ionic solid | A crystalline solid composed of ions | Solids |
| ionization energy (IE) | The amount of energy required to remove an electron from an atom in the gas phase. | Periodic Trends |
| isolated system | A system that does not allow a transfer of energy or matter into or out of itself. | Energy |
| isomer | A molecule with the same molecular formula as another molecule but a different structure | Hydrocarbons |
| isothermal | A process that does not change the temperature | Phase Transitions: Melting, Boiling and Subliming |
| isotopes | Atoms of the same element that have different numbers of neutrons | Atomic Theory |
| joule | The SI unit of energy. | Energy |
| kelvin | The fundamental unit of temperature in SI | Other Units: Temperature and Density |
| ketone | A compound where the carbonyl carbon is attached to two carbon chains | Other Oxygen-Containing Functional Groups |
| kinetic energy | Energy due to motion | Kinetic-Molecular Theory of Gases |
| kinetic molecular theory of gases | A model that helps us understand gases at the molecular level and their physical properties | Kinetic-Molecular Theory of Gases |
| kinetics | The study of reaction rate and the factors that can influence reaction rate | Introduction to Kinetics |
| law of conservation of energy | Law of physics that states that the total energy of an isolated system does not increase or decrease. | Energy |
| law of mass action | The relationship of the amounts of reactants and products at equilibrium | The Equilibrium Constant |
| Le Chatelier’s principle | If an equilibrium is stressed, then the reaction shifts to reduce the stress | Shifting Equilibria: Le Chatelier’s Principle |
| Lewis diagram | A representation of the valence electrons of an atom that uses dots around the symbol of the element. | Lewis Electron Dot Diagrams |
| limiting reagent | The reactant that runs out first for a given chemical reaction | Limiting Reagents |
| line spectrum | An image that contains only certain colors of light | Quantum Numbers for Electrons |
| locant | The numerical position of a substituent | Branched Hydrocarbons |
| lock and key model | A simple model used to describe enzyme activity, where substrates must fit into appropriately shaped active sites | Catalysis |
| lone electron pairs | A pair of electrons that does not make a covalent bond | Covalent Bonds |
| LUMO | The lowest unoccupied molecular orbital | Molecular Orbitals |
| magnetic quantum number (mℓ) | The index that determines the orientation of the electron’s spatial distribution. | Quantum Numbers for Electrons |
| mass-mass calculation | A calculation in which you start with a given mass of a substance and calculate the mass of another substance involved in the chemical equation | Mole-Mass and Mass-Mass Calculations |
| matter | Anything that has mass and takes up space. | Some Basic Definitions |
| mean free path | The average distance travelled by a molecule between collisions. | Molecular Effusion and Diffusion |
| melting | The process of a solid becoming a liquid | Phase Transitions: Melting, Boiling and Subliming |
| melting point | The characteristic temperature at which a solid becomes a liquid | Phase Transitions: Melting, Boiling and Subliming |
| meniscus | The curved surface a liquid makes as it approaches a solid barrier | Properties of Liquids |
| metal | An element that conducts electricity and heat well and is shiny, silvery, solid, ductile, and malleable | Some Basic Definitions |
| metallic solid | A solid with the characteristic properties of a metal | Solids |
| microstate (W) | A term used to describe different possible arrangements of molecular position and kinetic energy, at a particular thermodynamic state | Entropy and the Second Law of Thermodynamics |
| millimeters of mercury (mmHg) | The amount of pressure exerted by a column of mercury exactly 1 mm high | Pressure |
| mixture | A physical combination of more than one substance | Some Basic Definitions |
| molality (m) | The number of moles of solute per kilogram of solvent | Quantitative Units of Concentration |
| molar mass | The mass of 1 mol of a substance in grams | The Mole |
| molar volume | The volume of exactly 1 mol of a gas; equal to 22.4 L at STP. | The Ideal Gas Law and Some Applications |
| molarity (M) | The number of moles of solute divided by the number of liters of solution | Quantitative Units of Concentration |
| mole | The number of things equal to the number of atoms in exactly 12 g of carbon-12; equals 6.022×1023 things | The Mole |
| mole fraction | The ratio of the number of moles of a component in a mixture divided by the total number of moles in the sample | Gas Mixtures |
| mole fraction | The ratio of the number of moles of a component to the total number of moles in a system | Colligative Properties of Solutions |
| molecular formula | A formal listing of what and how many atoms are in a molecule | Molecules an Chemical Nomenclature |
| molecular geometry | how the atoms in a molecule are arranged | Molecular Shapes and Polarity |
| molecular mass | The sum of the masses of the atoms in a molecule | Masses of Atoms and Molecules |
| molecular orbital theory (MO theory) | A more sophisticated model of chemical bonding where new molecular orbitals are generated using a mathematical process called Linear Combination of Atomic Orbitals (LCAO) | Molecular Orbitals |
| molecular polarity | The vector sum of the individual bond dipoles | Molecular Shapes and Polarity |
| molecular solid | A crystalline solid whose components are covalently bonded molecules | Solids |
| molecularity | The total number of molecules that participate in the effective collision of the elementary step | Reaction Mechanisms |
| molecule | The smallest part of a substance that has the physical and chemical properties of that substance | Molecules an Chemical Nomenclature |
| mole-mass calculation | A calculation in which you start with a given number of moles of a substance and calculate the mass of another substance involved in the chemical equation, or vice versa | Mole-Mass and Mass-Mass Calculations |
| mole-mole calculation | A stoichiometry calculation when one starts with moles of one substance and convert to moles of another substance using the balanced chemical equation | The Mole in Chemical Reactions |
| monomer | The repeated unit of a polymer | Polymers |
| net ionic equation | A chemical equation with the spectator ions removed | Ionic Equations: A Closer Look |
| neutral salt | An ionic compound that does not affect the acidity of its aqueous solution | Strong and Weak Acids and Bases and Their Salts |
| neutralization reaction | The reaction of an acid with a base to produce water and a salt | Neutralization Reactions |
| neutron | A subatomic particle with no charge | Atomic Theory |
| node (nodal plane) | An area of zero electron density | Molecular Orbitals |
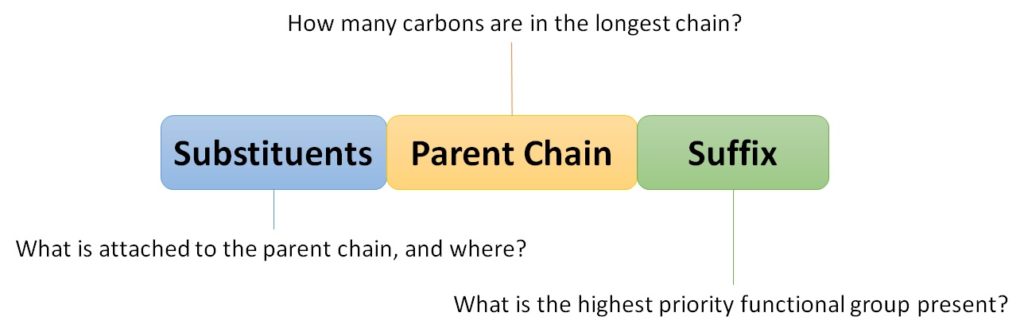
| nomenclature | The rules of naming in organic chemistry | Branched Hydrocarbons |
| nonmetal | An element that exists in various colors and phases, is brittle, and does not conduct electricity or heat well | Some Basic Definitions |
| nonpolar covalent bond | The equal sharing of electrons in a covalent bond | Other Aspects of Covalent Bonding |
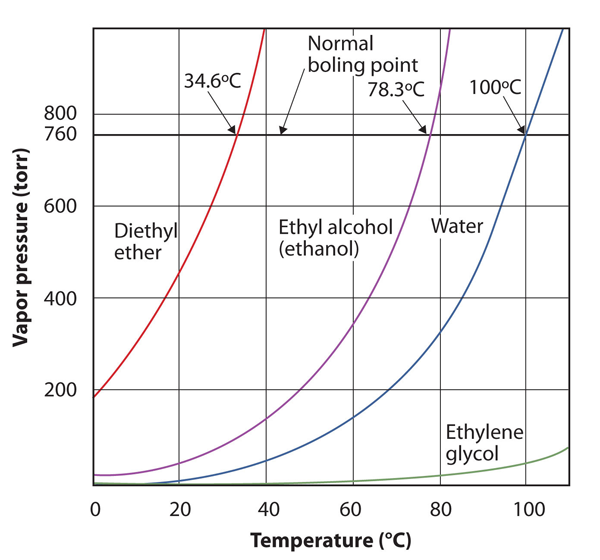
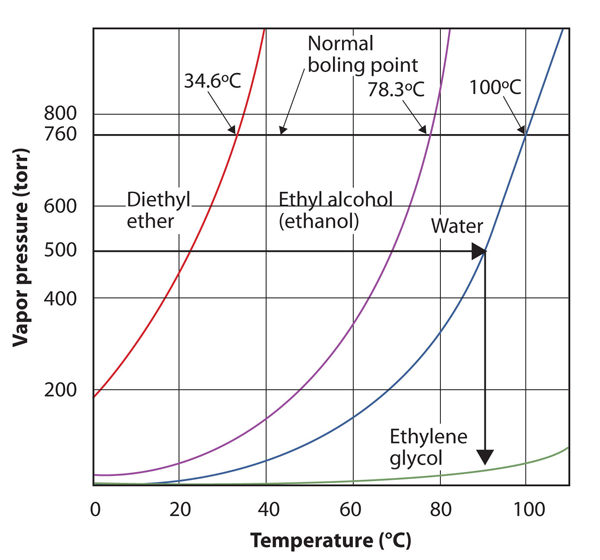
| normal boiling point | The characteristic temperature at which a liquid becomes a gas when the surrounding pressure is exactly 1 atm | Phase Transitions: Melting, Boiling and Subliming |
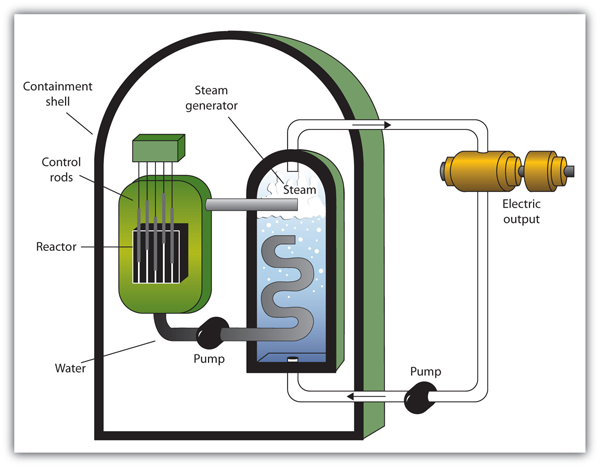
| nuclear energy | The controlled harvesting of energy from fission reactions | Nuclear Energy |
| nuclear equation | A chemical equation that emphasizes changes in atomic nuclei | Radioactivity |
| nuclear model | The model of an atom that has the protons and neutrons in a central nucleus with the electrons in orbit about the nucleus | Atomic Theory |
| nucleus | The centre of an atom that contains protons and neutrons | Atomic Theory |
| odd-electron molecules | A molecule with an odd number of electrons in the valence shell of an atom | Violations of the Octet Rule |
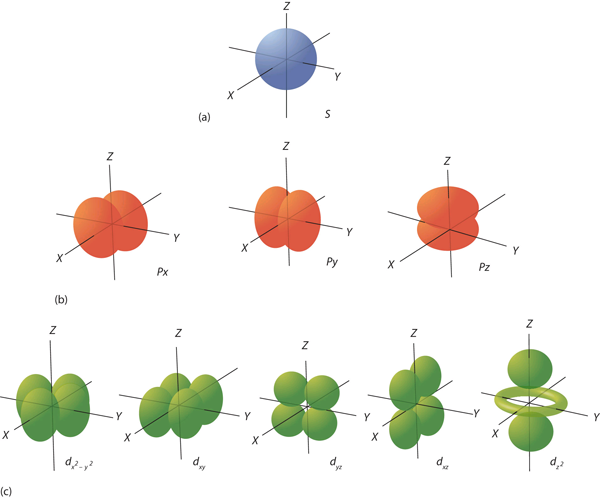
| orbital | The specific set of principal, angular momentum, and magnetic quantum numbers for an electron. | Quantum Numbers for Electrons |
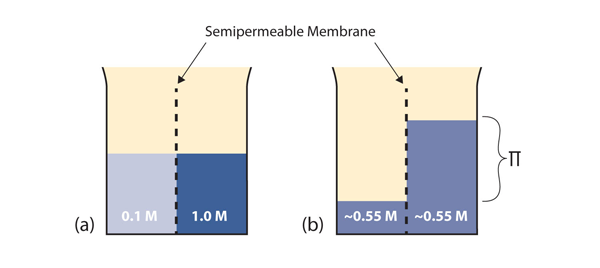
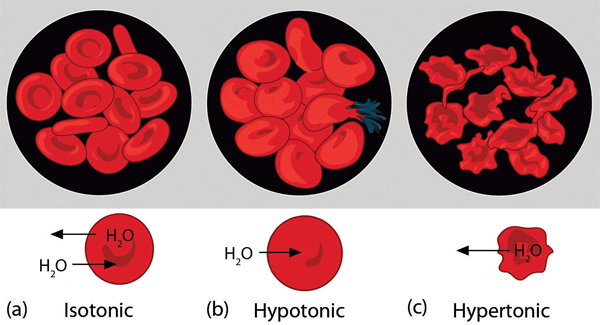
| osmosis | The tendency of solvent molecules to pass through a semipermeable membrane due to concentration differences | Colligative Properties of Solutions |
| osmotic pressure | The tendency of a solution to pass solvent through a semipermeable membrane due to concentration differences | Colligative Properties of Solutions |
| oxidation | The loss of one or more electrons by an atom; an increase in oxidation number | Oxidation-Reduction Reactions |
| oxidation number | A number assigned to an atom that helps keep track of the number of electrons on the atom | Oxidation-Reduction Reactions |
| oxidation-reduction (redox) reactions | A chemical reaction that involves the transfer of electrons | Oxidation-Reduction Reactions |
| p block | The columns of the periodic table in which p subshells are being occupied. | Electronic Structure and the Periodic Table |
| parent isotope | The reactant in a nuclear equation | Radioactivity |
| parts per billion (ppb) | Ratio of mass of solute to total mass of sample times 1,000,000,000 | Quantitative Units of Concentration |
| parts per million (ppm) | Ratio of mass of solute to total mass of sample times 1,000,000 | Quantitative Units of Concentration |
| parts per thousand (ppth) | Ratio of mass of solute to total mass of sample times 1,000 | Quantitative Units of Concentration |
| Pauli exclusion principle | No two electrons in an atom can have the same set of four quantum numbers. | Organization of Electrons in Atoms |
| percent yield | Actual yield divided by theoretical yield times 100% to give a percentage between 0% and 100% | Yields |
| percentage composition by mass (or mass percentage, % m/m) | Ratio of mass of solute to the total mass of a sample times 100 | Quantitative Units of Concentration |
| periodic table | A chart of all the elements | Atomic Theory |
| periodic trends | The variation of properties versus position on the periodic table. | Periodic Trends |
| pH | The negative logarithm of the hydrogen ion concentration | The pH Scale |
| pH scale | The range of values from 0 to 14 that describes the acidity or basicity of a solution | The pH Scale |
| phase | An important physical property that defines whether matter is a solid, liquid, gas or supercritical fluid | Some Basic Definitions |
| phase diagram | A graphical representation of the equilibrium relationships that exist between the phases of a substance under specified pressures and temperatures | Properties of Liquids |
| photon | The name of a discrete unit of light acting as a particle. | Light |
| physical change | A change that occurs when a sample of matter changes one or more of its physical properties | Some Basic Definitions |
| physical property | A characteristic that describes matter as it exists | Some Basic Definitions |
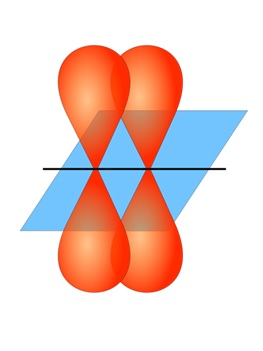
| pi bond (π bond) | The sideways overlap of p orbitals, placing electron density on opposite sides of the inter-nuclear axis – a double or triple bond | Valence Bond Theory and Hybrid Orbitals |
| Planck’s constant | The proportionality constant between the frequency and the energy of light: 6.626 × 10 to the power of −34 J·s. | Light |
| pOH | The negative logarithm of the hydroxide ion concentration | The pH Scale |
| polar covalent bond | A covalent bond between different atoms that attract the shared electrons by different amounts and cause an imbalance of electron distribution | Other Aspects of Covalent Bonding |
| polarity | A measure of the unequal sharing of electrons which has resulted in a dipole moment | Other Aspects of Covalent Bonding |
| polyatomic ions | An ion that contains more than one atom | Ions and Ionic Compounds |
| polymer | A long molecule made of many repeating units | Polymers |
| polymerization | The process of making a polymer | Polymers |
| polyprotic acid | An acid capable of donating more than one H+ ion | Some Special Types of Equilibria |
| precipitate | A solid that falls out of solution in a precipitation reaction | Types of Chemical Reactions: Single- and Double-Displacement Reactions |
| precipitation reaction | A chemical reaction in which two ionic compounds are dissolved in water and form a new ionic compound that does not dissolve | Types of Chemical Reactions: Single- and Double-Displacement Reactions |
| prefix | A prefix used with a unit that refers to a multiple or fraction of a fundamental unit to make a more conveniently sized unit for a specific quantity | Expressing Units |
| pressure | Force per unit area | Pressure |
| primary battery | A battery that cannot be recharged | Applications of Redox Reactions: Voltaic Cells |
| principal quantum number (n) | The index that largely determines the energy of an electron in an atom. | Quantum Numbers for Electrons |
| product | A final substance in a chemical equation | The Chemical Equation |
| proton | A subatomic particle with a positive charge | Atomic Theory |
| qualitative | A description of the quality of an object | Chemistry as a Science |
| quantitative | A description of a specific amount of something | Chemistry as a Science |
| quantization | When a quantity is restricted to having only certain values. | Quantum Numbers for Electrons |
| quantum mechanics | The theory of electrons that treats them as a wave. | Quantum Numbers for Electrons |
| quantum number | An index that corresponds to a property of an electron, like its energy. | Quantum Numbers for Electrons |
| rad | A unit of radioactive exposure equal to 0.01 J/g of tissue | Units of Radioactivity |
| radioactive decay | The spontaneous change of a nucleus from one element to another | Radioactivity |
| radioactivity | Emanations of particles and radiation from atomic nuclei | Radioactivity |
| Raoult’s law | The mathematical formula for calculating the vapor pressure of a solution | Colligative Properties of Solutions |
| rate constant (k) | A proportionality constant specific to each reaction at a particular temperature | Rate Laws |
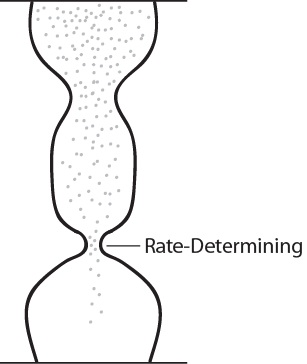
| rate-determining step | The slowest step in a multistep mechanism | Reaction Mechanisms |
| rate law | A mathematical relationship between the reaction rate and the reactant concentrations | Rate Laws |
| reactant | An initial substance in a chemical equation | The Chemical Equation |
| reaction mechanism | The bond making and bond breaking steps which occur at the molecular level during a chemical reaction | Reaction Mechanisms |
| reaction order | The sum of the concentration term exponents in a rate law equation | Rate Laws |
| reaction rate | The speed of a chemical reaction | Introduction to Kinetics |
| real gas | A gas that deviates from ideal behaviour. | Real Gases |
| redox reaction | A chemical reaction that involves the transfer of electrons | Oxidation-Reduction Reactions |
| reduction | The gain of one or more electrons by an atom; a decrease in oxidation number | Oxidation-Reduction Reactions |
| rem | A unit of radioactive exposure that includes a factor to account for the type of radioactivity | Units of Radioactivity |
| ribozyme | Ribonucleic acid (RNA) molecules capable of catalyzing certain chemical reactions | Catalysis |
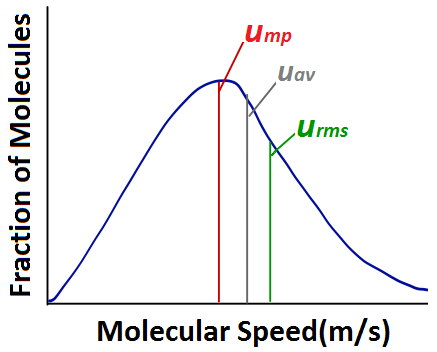
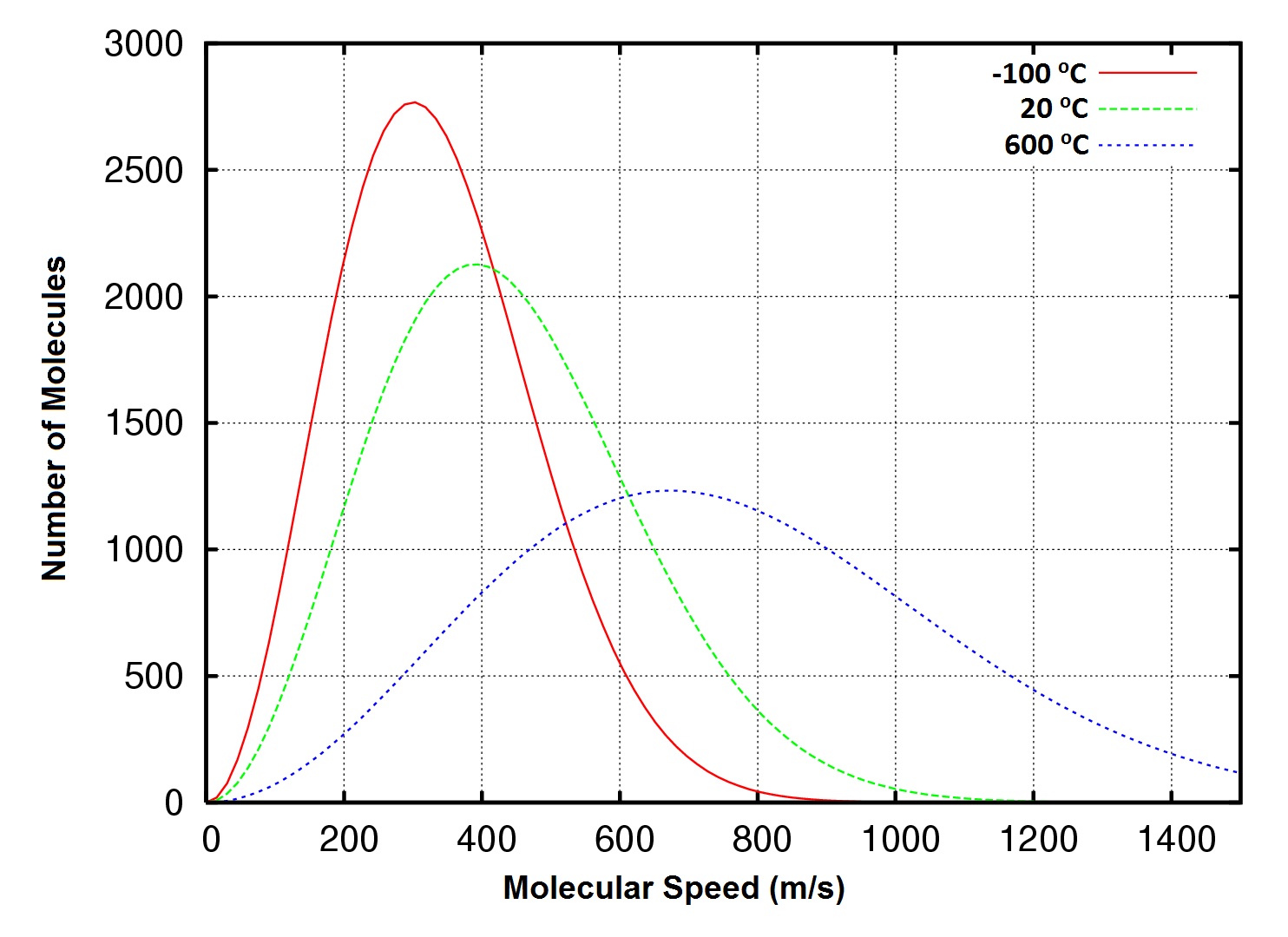
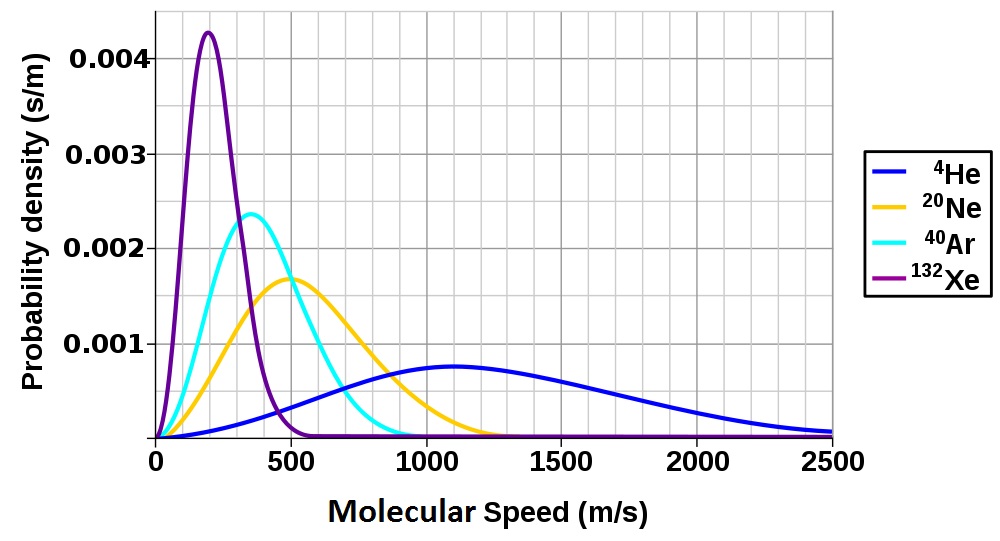
| root-mean-square (rms) speed (urms) | The speed of molecules having exactly the same kinetic energy as the average kinetic energy of the sample | Kinetic-Molecular Theory of Gases |
| s block | The columns of the periodic table in which s subshells are being occupied | Electronic Structure and the Periodic Table |
| salt | Any ionic compound that is formed from a reaction between an acid and a base | Neutralization Reactions |
| salt | Any ionic compound that is formed from a reaction between an acid and a base | Arrhenius Acids and Bases |
| salt bridge | A part of a voltaic cell that contains a solution of some ionic compound whose ions migrate to either side of the voltaic cell to maintain the charge balance | Applications of Redox Reactions: Voltaic Cells |
| saturated hydrocarbons | A carbon compound with the maximum possible number of H atoms in its formula | Hydrocarbons |
| saturated solution | A solution with the maximum amount of solute dissolved in it | Some Definitions |
| science | The process of knowing about the natural universe through observation and experiment | Chemistry as a Science |
| scientific law | A specific statement that is thought to be never violated by the entire natural universe | Chemistry as a Science |
| scientific notation | An expression of a number using powers of 10 | Expressing Numbers |
| screening | The repelling valence electrons by core electrons | Periodic Trends |
| second law of thermodynamics | A spontaneous process will increase the entropy of the universe | Entropy and the Second Law of Thermodynamics |
| secondary battery | A battery that can be recharged | Applications of Redox Reactions: Voltaic Cells |
| semimetal | An element that has properties of both metals and nonmetals | Some Basic Definitions |
| semipermeable membrane | A thin membrane that will pass certain small molecules but not others | Colligative Properties of Solutions |
| SI unit | International System of Units used by all scientists, literally translated from “le Système International d’unités.” | Expressing Units |
| Sievert (Sv) | Sievert (Sv) is a related unit and is defined as 100 rem | Units of Radioactivity |
| sigma bond (σ bond) | Orbital overlap to form a bond which has cylindrical symmetry – a single bond | Valence Bond Theory and Hybrid Orbitals |
| significant figures | The limit of the number of places a measurement can be properly expressed with | Significant Figures |
| silicones | A polymer based on a silicon and oxygen backbone | Polymers |
| single bond | A covalent bond composed of one pair of electrons | Covalent Bonds |
| single-replacement reaction | A chemical reaction in which one element is substituted for another element in a compound | Types of Chemical Reactions: Single- and Double-Displacement Reactions |
| solidification | The process of a liquid becoming a solid | Phase Transitions: Melting, Boiling and Subliming |
| solubility | The maximum amount of a solute that can be dissolved in a given amount of a solvent | Some Definitions |
| solubility rules | General statements that predict which ionic compounds dissolve and which do not | Types of Chemical Reactions: Single- and Double-Displacement Reactions |
| solute | The minor component of a solution | Some Definitions |
| solution | See homogeneous mixture | Some Basic Definitions |
| solvent | The major component of a solution. | Some Definitions |
| specific heat capacity | The proportionality constant between heat, mass, and temperature change; also called specific heat. | Work and Heat |
| spectator ion | An ion that does nothing in the overall course of a chemical reaction | Ionic Equations: A Closer Look |
| spin quantum number (m_s) | The index that indicates one of two spin states for an electron. | Quantum Numbers for Electrons |
| spontaneous process | A process that occurs without the influence of external forces or a change that moves a system towards equilibrium | Spontaneous Change |
| standard molar entropy (So) | The entropy of 1 mole of a substance in its standard state, at 1 atm of pressure | Measuring Entropy and Entropy Changes |
| standard notation | A straightforward expression of a number | Expressing Numbers |
| standard temperature and pressure (STP) | A set of benchmark conditions used to compare other properties of gases: 100 kPa for pressure and 273 K for temperature | The Ideal Gas Law and Some Applications |
| stoichiometry | The relating of one chemical substance to another using a balanced chemical reaction | Stoichiometry |
| strong acid | Any acid that is 100% dissociated into ions in aqueous solution | Strong and Weak Acids and Bases and Their Salts |
| strong base | Any base that is 100% dissociated into ions in aqueous solution | Strong and Weak Acids and Bases and Their Salts |
| sublimation | The process of a solid becoming a gas | Phase Transitions: Melting, Boiling and Subliming |
| subshell | A term used to describe electrons in a shell that have the same angular momentum quantum number. | Quantum Numbers for Electrons |
| substance | Matter that has the same physical and chemical properties throughout. | Some Basic Definitions |
| substituent | A branch off a main chain in a hydrocarbon | Branched Hydrocarbons |
| substrate | The reactants which are specific for a biological catalyst | Catalysis |
| supercritical fluid | A phase beyond the critical point, where liquid and gas phases are no longer distinct | Properties of Liquids |
| supersaturated solution | A unstable solution with more than the normal maximum amount of solute in it | Some Definitions |
| surface tension | An effect caused by an imbalance of forces on the atoms at the surface of a liquid | Properties of Liquids |
| surrounding atoms | An atom that makes covalent bonds to the central atom(s) | Covalent Bonds |
| system | The part of the universe that is under study. | Energy |
| temperature | A measure of the average amount of kinetic energy a system contains | Other Units: Temperature and Density |
| theoretical yield | An amount that is theoretically produced as calculated using the balanced chemical reaction | Yields |
| theory | A general statement that explains a large number of observations | Chemistry as a Science |
| thermochemical equation | A chemical equation that includes an enthalpy change. | Enthalpy and Chemical Reactions |
| thiol | The sulfur analog of an alcohol | Other Functional Groups |
| third law of thermodynamics | At absolute zero the entropy of a pure, perfect crystal is zero | Measuring Entropy and Entropy Changes |
| titrant | The reagent of known concentration | Acid-Base Titrations |
| titration | A chemical reaction performed quantitatively to determine the exact amount of a reagent | Acid-Base Titrations |
| torr | Another name for a millimeter of mercury | Pressure |
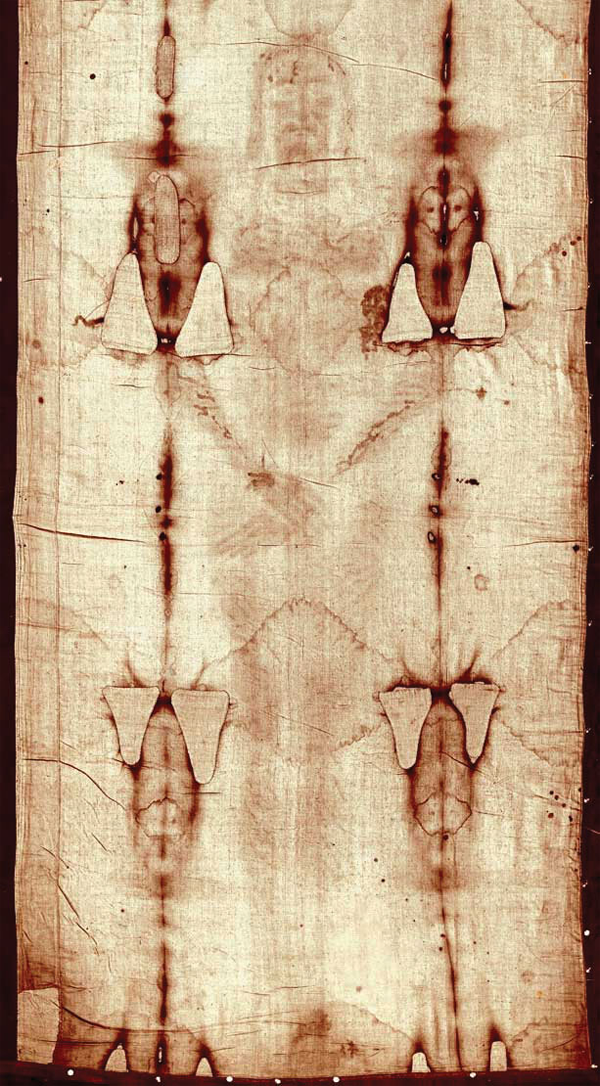
| tracer | A substance that can be used to follow the pathway of that substance through a structure | Uses of Radioactive Isotopes |
| transition state | The highest energy transitional point in the elementary step | Reaction Mechanisms |
| triple bond | A covalent bond composed of three pairs of bonding electrons | Covalent Bonds |
| unsaturated hydrocarbons | A carbon compound with less than the maximum possible number of H atoms in its formula | Hydrocarbons |
| unsaturated solution | A solution with less than the maximum amount of solute dissolved in it | Some Definitions |
| valence electron | An electron in the highest-numbered shell or in the last unfilled subshell. Valence electrons are those that are most likely to be involved in chemical reactions. | Electronic Structure and the Periodic Table |
| valence shell | The highest-numbered shell in an atom that contains electrons. | Electronic Structure and the Periodic Table |
| valence shell electron pair repulsion theory (VSEPR) | The general concept that estimates the shape of a simple molecule: electron pairs repel each other to get as far away from each other as possible | Molecular Shapes and Polarity |
| van der Waals equation | An equation that compensates for deviations from ideal gas behaviour, correcting for intermolecular forces and the volume of gas molecules. | Real Gases |
| van’t Hoff factor (i) | The number of particles each solute formula unit breaks apart into when it dissolves | Colligative Properties of Ionic Solutes |
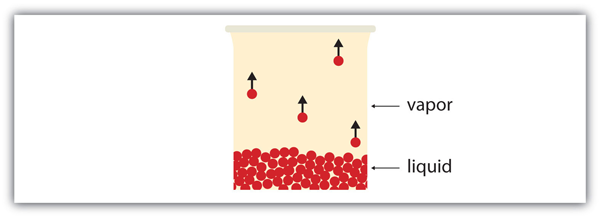
| vapor | Material in the gas phase due to evaporation | Properties of Liquids |
| vapor pressure | The partial pressure exerted by evaporation of a liquid | Gas Mixtures |
| vapor pressure depression | The decrease of a solution’s vapor pressure because of the presence of a solute | Colligative Properties of Solutions |
| vector quantity | A quantity which has both a magnitude and direction | Molecular Shapes and Polarity |
| voltaic (galvanic) cell | An apparatus that allows for useful electrical work to be extracted from a redox reaction. | Applications of Redox Reactions: Voltaic Cells |
| wavelength | The distance between corresponding points in two adjacent light cycles. | Light |
| weak acid | Any acid that is less than 100% dissociated into ions in aqueous solution | Strong and Weak Acids and Bases and Their Salts |
| weak base | Any base that is less than 100% dissociated into ions in aqueous solution | Strong and Weak Acids and Bases and Their Salts |






















































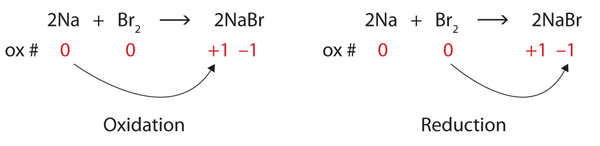















![Plot of 1/[C] versus time for a second-order reaction.](https://opentextbc.ca/introductorychemistry/wp-content/uploads/sites/17/2021/06/Second-order-reaction-plot-1.jpg)



 Dr. Jessie Key is a professor of chemistry at Vancouver Island University in Nanaimo, British Columbia. He received his Ph.D from the University of Alberta in Edmonton, Alberta, and his B.Sc (Hons.) from Thompson Rivers University in Kamloops, British Columbia. Jessie’s main area of research expertise is chemical biology; with a focus on fluorophore synthesis, cellular labelling and bioassays. He currently teaches general chemistry and organic chemistry at Vancouver Island University, and does research on the use of technology in chemical education.
Dr. Jessie Key is a professor of chemistry at Vancouver Island University in Nanaimo, British Columbia. He received his Ph.D from the University of Alberta in Edmonton, Alberta, and his B.Sc (Hons.) from Thompson Rivers University in Kamloops, British Columbia. Jessie’s main area of research expertise is chemical biology; with a focus on fluorophore synthesis, cellular labelling and bioassays. He currently teaches general chemistry and organic chemistry at Vancouver Island University, and does research on the use of technology in chemical education. Dr. Ball is a professor of chemistry at Cleveland State University in Ohio. He earned his PhD from Rice University in Houston, Texas. His specialty is physical chemistry, which he teaches at the undergraduate and graduate levels. About 50 percent of his teaching is in general chemistry: chemistry for nonscience majors, GOB, and general chemistry for science and engineering majors. In addition to this text, he is the author of a math review book for general chemistry students, a physical chemistry textbook with accompanying student and instructor solutions manuals, and two books on spectroscopy (published by SPIE Press). He is coauthor of a general chemistry textbook (with Dan Reger and Scott Goode), whose third edition was published in January 2009. His publication list has over 180 items, roughly evenly distributed between research papers and articles of educational interest.
Dr. Ball is a professor of chemistry at Cleveland State University in Ohio. He earned his PhD from Rice University in Houston, Texas. His specialty is physical chemistry, which he teaches at the undergraduate and graduate levels. About 50 percent of his teaching is in general chemistry: chemistry for nonscience majors, GOB, and general chemistry for science and engineering majors. In addition to this text, he is the author of a math review book for general chemistry students, a physical chemistry textbook with accompanying student and instructor solutions manuals, and two books on spectroscopy (published by SPIE Press). He is coauthor of a general chemistry textbook (with Dan Reger and Scott Goode), whose third edition was published in January 2009. His publication list has over 180 items, roughly evenly distributed between research papers and articles of educational interest.