active power: The power dissipated in the form of heat or light when dealing with a purely resistive circuit. It is also known as true power.
acute angle: An angle that is less than 90 degrees.
adjacent: The side of a triangle that sits adjacent to the designate angle.
angle: The space between two intersecting lines.
armature: The part of an alternator where the voltage is induced on to. It can be rotating (simple alternator) or stationary (practical alternator).
brushes: The parts of an alternator that are made of graphite carbon. They are stationary and either pass current to the load (simple alternator) or current to the field (practical alternator).
complementary angles: Two angles whose sum equals 90 degrees.
CPS: Short for cycles per second, used to measure frequency.
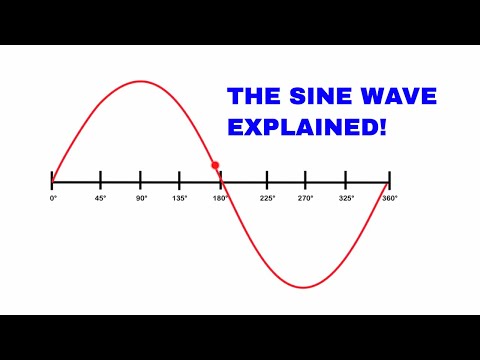
cycle: From the point in a waveform to where the waveform starts to repeat itself.
degree: One-three-hundred-and-sixtieth of the circumference of a circle. It is also the unit by which we measure angles.
designate angle (or theta): An angle that you determine or is determined for you, and upon which triangle sides (adjacent, hypotenuse, opposite) are named and dependent.
electromagnetic induction: When a voltage is created by passing a conductor through a magnetic field.
equilateral triangle: All three sides of this triangle are equal, and all three of its angles are equal too.
field poles: The parts of an alternator that are either stationary (simple alternator) or rotating (practical alternator).
frequency: The number of cycles can occur in one second. Frequency is measured in hertz or CPS (cycles per second).
hertz (Hz): The unit used us measure frequency.
hypotenuse: The side of a triangle that sits opposite the right, or 90-degree, angle. It is always the longest side of the triangle.
imaginary numbers: A term referring to components that don’t really exist such as X and Y.
impedance: A total opposition to current flow determined by adding reactance to resistance using the Pythagoras’ theorem.
impedance triangle: The triangle that is created when the resistance is added to the reactance.
isosceles triangle: This triangle has two sides that are equal, and two angles that are equal.
obtuse angle: An angle that is greater than 90 degrees.
opposite: The side of a triangle that sits opposite to the designate angle.
point of origin: A reference point.
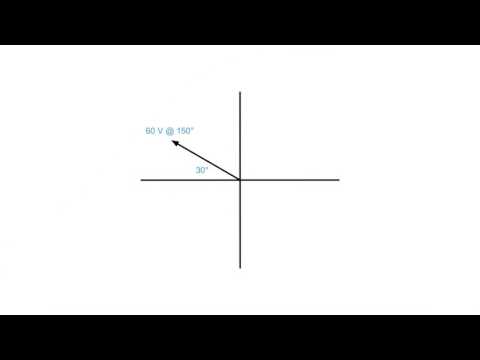
polar form: An expression of vectors using magnitude and direction. See rectangular form.
practical alternator: Has a stationary conductor and the field rotates in order to maintain voltage. See simple alternator.
prime mover: The part of an alternator that spins the armature (simple) or the field (practical). Examples include combustion engine, hydro dam, hand crank and windmill.
Pythagorean theorem/Pythagoras’ theorem: A relation in Euclidean geometry among the three sides of a right triangle. It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. In simple terms, this theorem says that you can figure out any side of a right triangle as long as you have the other two sides, using the equation:
A2 + B2 = C2
quadrant: A circle cut into four parts.
quadrature power: See reactive power.
reactance: The component that opposes current in an AC circuit. This runs 90 degrees to circuit resistance.
reactive power: The power that is present when current passes across the reactance. It is also known as wattless or quadrature power.
rectangular form: An expression of vectors using X and Y coordinates. See polar form.
resistance: The component that opposes current in a DC circuit.
resultant: The sum of the vectors.
right angle: An angle that equals 90 degrees.
RPM: Short for rotations per minute, used to measure a machine’s rotational speed.
RPS: Short for rotations per second.
similar angles: These triangles each have different sized sides, but share the same sized angles. See practical alternator.
simple alternator: When a conductor is formed into a loop and rotates through a field to maintain voltage.
slip rings: The parts of an alternator that are made of brass. They rotate and either bring current to the load (simple alternator) or excitation to the field (practical alternator).
supplementary angles: Two angles whose sum equals 180 degrees.
theta: See designate angle.
trigonometry: The study of the relationship that exists between the sides and the angles of a triangle.
true power: See active power.
vector: A quantity that possesses magnitude and direction.
vectorially: Related to or involving vectors.
wattless power: See reactive power.