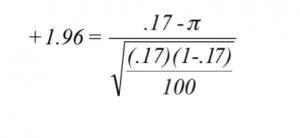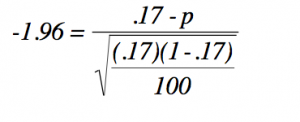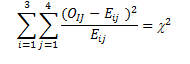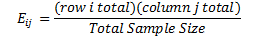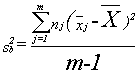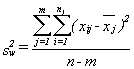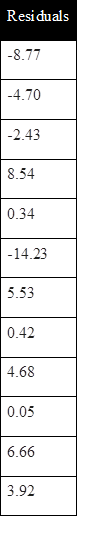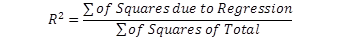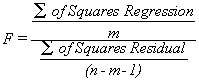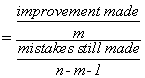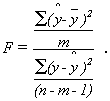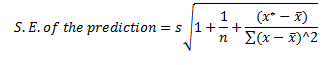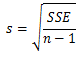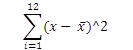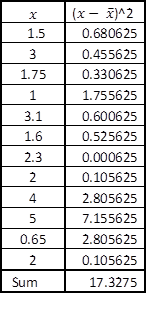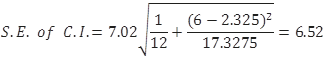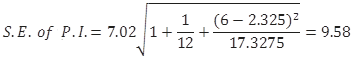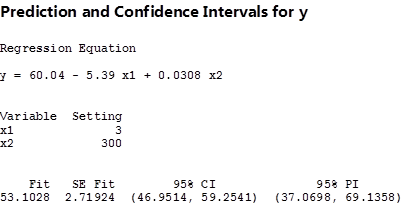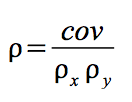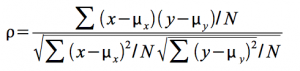Regression analysis, like most multivariate statistics, allows you to infer that there is a relationship between two or more variables. These relationships are seldom exact because there is variation caused by many variables, not just the variables being studied.
If you say that students who study more make better grades, you are really hypothesizing that there is a positive relationship between one variable, studying, and another variable, grades. You could then complete your inference and test your hypothesis by gathering a sample of (amount studied, grades) data from some students and use regression to see if the relationship in the sample is strong enough to safely infer that there is a relationship in the population. Notice that even if students who study more make better grades, the relationship in the population would not be perfect; the same amount of studying will not result in the same grades for every student (or for one student every time). Some students are taking harder courses, like chemistry or statistics; some are smarter; some study effectively; and some get lucky and find that the professor has asked them exactly what they understood best. For each level of amount studied, there will be a distribution of grades. If there is a relationship between studying and grades, the location of that distribution of grades will change in an orderly manner as you move from lower to higher levels of studying.
Regression analysis is one of the most used and most powerful multivariate statistical techniques for it infers the existence and form of a functional relationship in a population. Once you learn how to use regression, you will be able to estimate the parameters — the slope and intercept — of the function that links two or more variables. With that estimated function, you will be able to infer or forecast things like unit costs, interest rates, or sales over a wide range of conditions. Though the simplest regression techniques seem limited in their applications, statisticians have developed a number of variations on regression that greatly expand the usefulness of the technique. In this chapter, the basics will be discussed. Once again, the t-distribution and F-distribution will be used to test hypotheses.
What is regression?
Before starting to learn about regression, go back to algebra and review what a function is. The definition of a function can be formal, like the one in my freshman calculus text: “A function is a set of ordered pairs of numbers (x,y) such that to each value of the first variable (x) there corresponds a unique value of the second variable (y)” (Thomas, 1960).. More intuitively, if there is a regular relationship between two variables, there is usually a function that describes the relationship. Functions are written in a number of forms. The most general is y = f(x), which simply says that the value of y depends on the value of x in some regular fashion, though the form of the relationship is not specified. The simplest functional form is the linear function where:
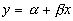
α and β are parameters, remaining constant as x and y change. α is the intercept and β is the slope. If the values of α and β are known, you can find the y that goes with any x by putting the x into the equation and solving. There can be functions where one variable depends on the values values of two or more other variables where x1 and x2 together determine the value of y. There can also be non-linear functions, where the value of the dependent variable (y in all of the examples we have used so far) depends on the values of one or more other variables, but the values of the other variables are squared, or taken to some other power or root or multiplied together, before the value of the dependent variable is determined. Regression allows you to estimate directly the parameters in linear functions only, though there are tricks that allow many non-linear functional forms to be estimated indirectly. Regression also allows you to test to see if there is a functional relationship between the variables, by testing the hypothesis that each of the slopes has a value of zero.
First, let us consider the simple case of a two-variable function. You believe that y, the dependent variable, is a linear function of x, the independent variable — y depends on x. Collect a sample of (x, y) pairs, and plot them on a set of x, y axes. The basic idea behind regression is to find the equation of the straight line that comes as close as possible to as many of the points as possible. The parameters of the line drawn through the sample are unbiased estimators of the parameters of the line that would come as close as possible to as many of the points as possible in the population, if the population had been gathered and plotted. In keeping with the convention of using Greek letters for population values and Roman letters for sample values, the line drawn through a population is:
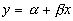
while the line drawn through a sample is:
y = a + bx
In most cases, even if the whole population had been gathered, the regression line would not go through every point. Most of the phenomena that business researchers deal with are not perfectly deterministic, so no function will perfectly predict or explain every observation.
Imagine that you wanted to study the estimated price for a one-bedroom apartment in Nelson, BC. You decide to estimate the price as a function of its location in relation to downtown. If you collected 12 sample pairs, you would find different apartments located within the same distance from downtown. In other words, you might draw a distribution of prices for apartments located at the same distance from downtown or away from downtown. When you use regression to estimate the parameters of price = f(distance), you are estimating the parameters of the line that connects the mean price at each location. Because the best that can be expected is to predict the mean price for a certain location, researchers often write their regression models with an extra term, the error term, which notes that many of the members of the population of (location, price of apartment) pairs will not have exactly the predicted price because many of the points do not lie directly on the regression line. The error term is usually denoted as ε, or epsilon, and you often see regression equations written:
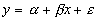
Strictly, the distribution of ε at each location must be normal, and the distributions of ε for all the locations must have the same variance (this is known as homoscedasticity to statisticians).
Simple regression and least squares method
In estimating the unknown parameters of the population for the regression line, we need to apply a method by which the vertical distances between the yet-to-be estimated regression line and the observed values in our sample are minimized. This minimized distance is called sample error, though it is more commonly referred to as residual and denoted by e. In more mathematical form, the difference between the y and its predicted value is the residual in each pair of observations for x and y. Obviously, some of these residuals will be positive (above the estimated line) and others will be negative (below the line). If we add all these residuals over the sample size and raise them to the power 2 in order to prevent the chance those positive and negative signs are cancelling each other out, we can write the following criterion for our minimization problem:
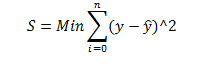
S is the sum of squares of the residuals. By minimizing S over any given set of observations for x and y, we will get the following useful formula:

After computing the value of b from the above formula out of our sample data, and the means of the two series of data on x and y, one can simply recover the intercept of the estimated line using the following equation:
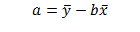
For the sample data, and given the estimated intercept and slope, for each observation we can define a residual as:
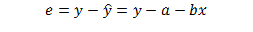
Depending on the estimated values for intercept and slope, we can draw the estimated line along with all sample data in a y–x panel. Such graphs are known as scatter diagrams. Consider our analysis of the price of one-bedroom apartments in Nelson, BC. We would collect data for y=price of one bedroom apartment, x1=its associated distance from downtown, and x2=the size of the apartment, as shown in Table 8.1.
Table 8.1 Data for Price, Size, and Distance of Apartments in Nelson, BC y = price of apartments in $1000
x1 = distance of each apartment from downtown in kilometres
x2 = size of the apartment in square feet |
| y | x1 | x2 |
| 55 | 1.5 | 350 |
| 51 | 3 | 450 |
| 60 | 1.75 | 300 |
| 75 | 1 | 450 |
| 55.5 | 3.1 | 385 |
| 49 | 1.6 | 210 |
| 65 | 2.3 | 380 |
| 61.5 | 2 | 600 |
| 55 | 4 | 450 |
| 45 | 5 | 325 |
| 75 | 0.65 | 424 |
| 65 | 2 | 285 |
The graph (shown in Figure 8.1) is a scatter plot of the prices of the apartments and their distances from downtown, along with a proposed regression line.
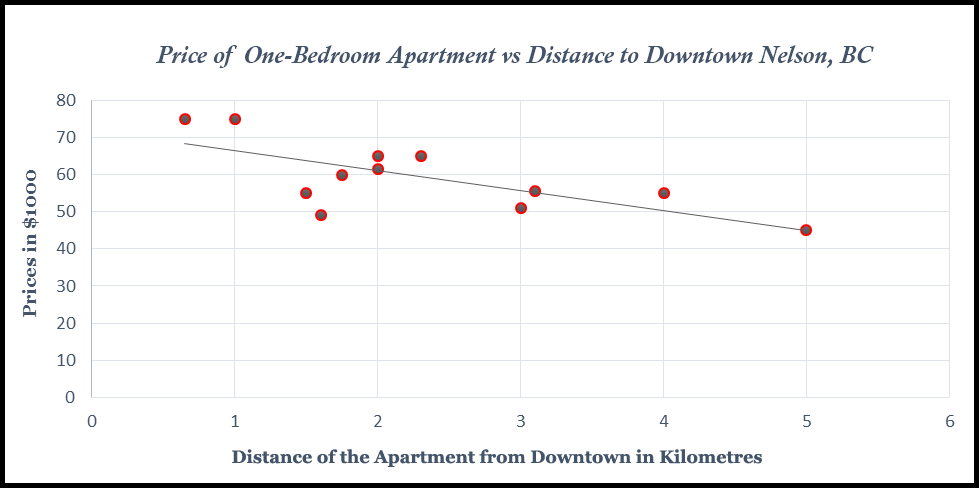
Figure 8.1 Scatter Plot of Price, Distance from Downtown, along with a Proposed Regression Line
In order to plot such a scatter diagram, you can use many available statistical software packages including Excel, SAS, and Minitab. In this scatter diagram, a negative simple regression line has been shown. The estimated equation for this scatter diagram from Excel is:
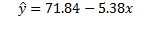
Where a=71.84 and b=-5.38. In other words, for every additional kilometre from downtown an apartment is located, the price of the apartment is estimated to be $5380 cheaper, i.e. 5.38*$1000=$5380. One might also be curious about the fitted values out of this estimated model. You can simply plug the actual value for x into the estimated line, and find the fitted values for the prices of the apartments. The residuals for all 12 observations are shown in Figure 8.2.
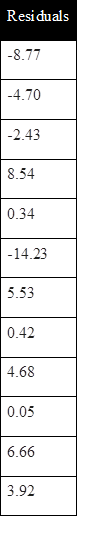
Figure 8.2
You should also notice that by minimizing errors, you have not eliminated them; rather, this method of least squares only guarantees the best fitted estimated regression line out of the sample data.
In the presence of the remaining errors, one should be aware of the fact that there are still other factors that might not have been included in our regression model and are responsible for the fluctuations in the remaining errors. By adding these excluded but relevant factors to the model, we probably expect the remaining error will show less meaningful fluctuations. In determining the price of these apartments, the missing factors may include age of the apartment, size, etc. Because this type of regression model does not include many relevant factors and assumes only a linear relationship, it is known as a simple linear regression model.
Testing your regression: does y really depend on x?
Understanding that there is a distribution of y (apartment price) values at each x (distance) is the key for understanding how regression results from a sample can be used to test the hypothesis that there is (or is not) a relationship between x and y. When you hypothesize that y = f(x), you hypothesize that the slope of the line (β in y = α + βx + ε) is not equal to zero. If β was equal to zero, changes in x would not cause any change in y. Choosing a sample of apartments, and finding each apartment’s distance to downtown, gives you a sample of (x, y). Finding the equation of the line that best fits the sample will give you a sample intercept, α, and a sample slope, β. These sample statistics are unbiased estimators of the population intercept, α, and slope, β. If another sample of the same size is taken, another sample equation could be generated. If many samples are taken, a sampling distribution of sample β’s, the slopes of the sample lines, will be generated. Statisticians know that this sampling distribution of b’s will be normal with a mean equal to β, the population slope. Because the standard deviation of this sampling distribution is seldom known, statisticians developed a method to estimate it from a single sample. With this estimated sb, a t-statistic for each sample can be computed:
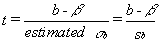
where n = sample size
m = number of explanatory (x) variables
b = sample slope
β= population slope
sb = estimated standard deviation of b’s, often called the standard error
These t’s follow the t-distribution in the tables with n–m-1 df.
Computing sb is tedious, and is almost always left to a computer, especially when there is more than one explanatory variable. The estimate is based on how much the sample points vary from the regression line. If the points in the sample are not very close to the sample regression line, it seems reasonable that the population points are also widely scattered around the population regression line and different samples could easily produce lines with quite varied slopes. Though there are other factors involved, in general when the points in the sample are farther from the regression line, sb is greater. Rather than learn how to compute sb, it is more useful for you to learn how to find it on the regression results that you get from statistical software. It is often called the standard error and there is one for each independent variable. The printout in Figure 8.3 is typical.

Figure 8.3 Typical Statistical Package Output for Linear Simple Regression Model
You will need these standard errors in order to test to see if y depends on x or not. You want to test to see if the slope of the line in the population, β, is equal to zero or not. If the slope equals zero, then changes in x do not result in any change in y. Formally, for each independent variable, you will have a test of the hypotheses:


If the t-score is large (either negative or positive), then the sample b is far from zero (the hypothesized β), and Ha should be accepted. Substitute zero for b into the t-score equation, and if the t-score is small, b is close enough to zero to accept Ha. To find out what t-value separates “close to zero” from “far from zero”, choose an alpha, find the degrees of freedom, and use a t-table from any textbook, or simply use the interactive Excel template from Chapter 3, which is shown again in Figure 8.4.
An interactive or media element has been excluded from this version of the text. You can view it online here: https://opentextbc.ca/introductorybusinessstatistics/?p=118
Figure 8.4 Interactive Excel Template for Determining t-Value from the t-Table – see Appendix 8.
Remember to halve alpha when conducting a two-tail test like this. The degrees of freedom equal n – m -1, where n is the size of the sample and m is the number of independent x variables. There is a separate hypothesis test for each independent variable. This means you test to see if y is a function of each x separately. You can also test to see if β > 0 (or β < 0) rather than β ≠ 0 by using a one-tail test, or test to see if β equals a particular value by substituting that value for β when computing the sample t-score.
Testing your regression: does this equation really help predict?
To test to see if the regression equation really helps, see how much of the error that would be made using the mean of all of the y’s to predict is eliminated by using the regression equation to predict. By testing to see if the regression helps predict, you are testing to see if there is a functional relationship in the population.
Imagine that you have found the mean price of the apartments in our sample, and for each apartment, you have made the simple prediction that price of apartment will be equal to the sample mean, y. This is not a very sophisticated prediction technique, but remember that the sample mean is an unbiased estimator of population mean, so on average you will be right. For each apartment, you could compute your error by finding the difference between your prediction (the sample mean, y) and the actual price of an apartment.
As an alternative way to predict the price, you can have a computer find the intercept, α, and slope, β, of the sample regression line. Now, you can make another prediction of how much each apartment in the sample may be worth by computing:

Once again, you can find the error made for each apartment by finding the difference between the price of apartments predicted using the regression equation ŷ, and the observed price, y. Finally, find how much using the regression improves your prediction by finding the difference between the price predicted using the mean, y, and the price predicted using regression, ŷ. Notice that the measures of these differences could be positive or negative numbers, but that error or improvement implies a positive distance.
Coefficient of Determination
If you use the sample mean to predict the amount of the price of each apartment, your error is (y–y) for each apartment. Squaring each error so that worries about signs are overcome, and then adding the squared errors together, gives you a measure of the total mistake you make if you want to predict y. Your total mistake is Σ(y–y)2. The total mistake you make using the regression model would be Σ(y-ŷ)2. The difference between the mistakes, a raw measure of how much your prediction has improved, is Σ(ŷ–y)2. To make this raw measure of the improvement meaningful, you need to compare it to one of the two measures of the total mistake. This means that there are two measures of “how good” your regression equation is. One compares the improvement to the mistakes still made with regression. The other compares the improvement to the mistakes that would be made if the mean was used to predict. The first is called an F-score because the sampling distribution of these measures follows the F-distribution seen in Chapter 6, “F-test and One-Way ANOVA”. The second is called R2, or the coefficient of determination.
All of these mistakes and improvements have names, and talking about them will be easier once you know those names. The total mistake made using the sample mean to predict, Σ(y–y)2, is called the sum of squares, total. The total mistake made using the regression, Σ(y-ŷ)2, is called the sum of squares, error (residual). The general improvement made by using regression, Σ(ŷ–y)2 is called the sum of squares, regression or sum of squares, model. You should be able to see that:
sum of squares, total = sum of squares, regression + sum of squares, error (residual)

In other words, the total variations in y can be partitioned into two sources: the explained variations and the unexplained variations. Further, we can rewrite the above equation as:
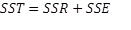
where SST stands for sum of squares due to total variations, SSR measures the sum of squares due to the estimated regression model that is explained by variable x, and SSE measures all the variations due to other factors excluded from the estimated model.
Going back to the idea of goodness of fit, one should be able to easily calculate the percentage of each variation with respect to the total variations. In particular, the strength of the estimated regression model can now be measured. Since we are interested in the explained part of the variations by the estimated model, we simply divide both sides of the above equation by SST, and we get:
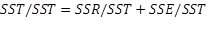
We then isolate this equation for the explained proportion, also known as R-square:
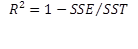
Only in cases where an intercept is included in a simple regression model will the value of R2 be bounded between zero and one. The closer R2 is to one, the stronger the model is. Alternatively, R2 is also found by:
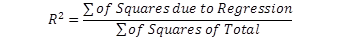
This is the ratio of the improvement made using the regression to the mistakes made using the mean. The numerator is the improvement regression makes over using the mean to predict; the denominator is the mistakes (errors) made using the mean. Thus R2 simply shows what proportion of the mistakes made using the mean are eliminated by using regression.
In the case of the market for one-bedroom apartments in Nelson, BC, the percentage of the variations in price for the apartments is estimated to be around 50%. This indicates that only half of the fluctuations in apartment prices with respect to the average price can be explained by the apartments’ distance from downtown. The other 50% are not controlled (that is, they are unexplained) and are subject to further research. One typical approach is to add more relevant factors to the simple regression model. In this case, the estimated model is referred to as a multiple regression model.
While R2 is not used to test hypotheses, it has a more intuitive meaning than the F-score. The F-score is the measure usually used in a hypothesis test to see if the regression made a significant improvement over using the mean. It is used because the sampling distribution of F-scores that it follows is printed in the tables at the back of most statistics books, so that it can be used for hypothesis testing. It works no matter how many explanatory variables are used. More formally, consider a population of multivariate observations, (y, x1, x2, …, xm), where there is no linear relationship between y and the x’s, so that y ≠ f(y, x1, x2, …, xm). If samples of n observations are taken, a regression equation estimated for each sample, and a statistic, F, found for each sample regression, then those F’s will be distributed like those shown in Figure 8.5, the F-table with (m, n–m-1) df.
An interactive or media element has been excluded from this version of the text. You can view it online here: https://opentextbc.ca/introductorybusinessstatistics/?p=118
Figure 8.5 Interactive Excel Template of an F-Table – see Appendix 8.
The value of F can be calculated as:
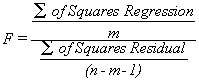
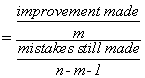
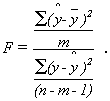
where n is the size of the sample, and m is the number of explanatory variables (how many x’s there are in the regression equation).
If Σ(ŷ–y)2 the sum of squares regression (the improvement), is large relative to Σ(ŷ–y)3, the sum of squares residual (the mistakes still made), then the F-score will be large. In a population where there is no functional relationship between y and the x’s, the regression line will have a slope of zero (it will be flat), and the ŷ will be close to y. As a result very few samples from such populations will have a large sum of squares regression and large F-scores. Because this F-score is distributed like the one in the F-tables, the tables can tell you whether the F-score a sample regression equation produces is large enough to be judged unlikely to occur if y ≠ f(y, x1, x2, …, xm). The sum of squares regression is divided by the number of explanatory variables to account for the fact that it always decreases when more variables are added. You can also look at this as finding the improvement per explanatory variable. The sum of squares residual is divided by a number very close to the number of observations because it always increases if more observations are added. You can also look at this as the approximate mistake per observation.

To test to see if a regression equation was worth estimating, test to see if there seems to be a functional relationship:

This might look like a two-tailed test since Ho has an equal sign. But, by looking at the equation for the F-score you should be able to see that the data support Ha only if the F-score is large. This is because the data support the existence of a functional relationship if the sum of squares regression is large relative to the sum of squares residual. Since F-tables are usually one-tail tables, choose an α, go to the F-tables for that α and (m, n–m-1) df, and find the table F. If the computed F is greater than the table F, then the computed F is unlikely to have occurred if Ho is true, and you can safely decide that the data support Ha. There is a functional relationship in the population.
Now that you have learned all the necessary steps in estimating a simple regression model, you may take some time to re-estimate the Nelson apartment model or any other simple regression model, using the interactive Excel template shown in Figure 8.6. Like all other interactive templates in this textbook, you can change the values in the yellow cells only. The result will be shown automatically within this template. For this template, you can only estimate simple regression models with 30 observations. You use special paste/values when you paste your data from other spreadsheets. The first step is to enter your data under independent and dependent variables. Next, select your alpha level. Check your results in terms of both individual and overall significance. Once the model has passed all these requirements, you can select an appropriate value for the independent variable, which in this example is the distance to downtown, to estimate both the confidence intervals for the average price of such an apartment, and the prediction intervals for the selected distance. Both these intervals are discussed later in this chapter. Remember that by changing any of the values in the yellow areas in this template, all calculations will be updated, including the tests of significance and the values for both confidence and prediction intervals.
An interactive or media element has been excluded from this version of the text. You can view it online here: https://opentextbc.ca/introductorybusinessstatistics/?p=118
Figure 8.6 Interactive Excel Template for Simple Regression – see Appendix 8.
Multiple Regression Analysis
When we add more explanatory variables to our simple regression model to strengthen its ability to explain real-world data, we in fact convert a simple regression model into a multiple regression model. The least squares approach we used in the case of simple regression can still be used for multiple regression analysis.
As per our discussion in the simple regression model section, our low estimated R2 indicated that only 50% of the variations in the price of apartments in Nelson, BC, was explained by their distance from downtown. Obviously, there should be more relevant factors that can be added into this model to make it stronger. Let’s add the second explanatory factor to this model. We collected data for the area of each apartment in square feet (i.e., x2). If we go back to Excel and estimate our model including the new added variable, we will see the printout shown in Figure 8.7.

Figure 8.7 Excel Printout
The estimates equation of the regression model is:
predicted price of apartments= 60.041 – 5.393*distance + .03*area
This is the equation for a plane, the three-dimensional equivalent of a straight line. It is still a linear function because neither of the x’s nor y is raised to a power nor taken to some root nor are the x’s multiplied together. You can have even more independent variables, and as long as the function is linear, you can estimate the slope, β, for each independent variable.
Before using this estimated model for prediction and decision-making purposes, we should test three hypotheses. First, we can use the F-score to test to see if the regression model improves our ability to predict price of apartments. In other words, we test the overall significance of the estimated model. Second and third, we can use the t-scores to test to see if the slopes of distance and area are different from zero. These two t-tests are also known as individual tests of significance.
To conduct the first test, we choose an α = .05. The F-score is the regression or model mean square over the residual or error mean square, so the df for the F-statistic are first the df for the regression model and, second, the df for the error. There are 2 and 9 df for the F-test. According to this F-table, with 2 and 9 df, the critical F-score for α = .05 is 4.26.
The hypotheses are:
H0: price ≠ f(distance, area)
Ha: price = f(distance, area)
Because the F-score from the regression, 6.812, is greater than the critical F-score, 4.26, we decide that the data support Ho and conclude that the model helps us predict price of apartments. Alternatively, we say there is such a functional relationship in the population.
Now, we move to the individual test of significance. We can test to see if price depends on distance and area. There are (n-m-1)=(12-2-1)=9 df. There are two sets of hypotheses, one set for β1, the slope for distance, and one set for β2, the slope for area. For a small town, one may expect that β1, the slope for distance, will be negative, and expect that β2 will be positive. Therefore, we will use a one-tail test on β1, as well as for β2:

Since we have two one-tail tests, the t-values we choose from the t-table will be the same for the two tests. Using α = .05 and 9 df, we choose .05/2=.025 for the t-score for β1 with a one-tail test, and come up with 2.262. Looking back at our Excel printout and checking the t-scores, we decide that distance does affect price of apartments, but area is not a significant factor in explaining the price of apartments. Notice that the printout also gives a t-score for the intercept, so we could test to see if the intercept equals zero or not.
Alternatively, one may go ahead and compare directly the p-values out of the Excel printout against the assumed level of significance (i.e., α = .05). We can easily see that the p-values associated with the intercept and price are both less than alpha, and as a result we reject the hypothesis that the associated coefficients are zero (i.e., both are significant). However, area is not a significant factor since its associated p-value is greater than alpha.
While there are other required assumptions and conditions in both simple and multiple regression models (we encourage students to consult an intermediate business statistics open textbook for more detailed discussions), here we only focus on two relevant points about the use and applications of multiple regression.
The first point is related to the interpretation of the estimated coefficients in a multiple regression model. You should be careful to note that in a simple regression model, the estimated coefficient of our independent variable is simply the slope of the line and can be interpreted. It refers to the response of the dependent variable to a one-unit change in the independent variable. However, this interpretation in a multiple regression model should be adjusted slightly. The estimated coefficients under multiple regression analysis are the response of the dependent variable to a one-unit change in one of the independent variables when the levels of all other independent variables are kept constant. In our example, the estimated coefficient of price of an apartment in Nelson, BC, indicates that — for a given size of apartment— it will drop by 5.248*1000=$5248 for every one kilometre that the apartment is away from downtown.
The second point is about the use of R2 in multiple regression analysis. Technically, adding more independent variables to the model will increase the value of R2, regardless of whether the added variables are relevant or irrelevant in explaining the variation in the dependent variable. In order to adjust the inflated R2 due to the irrelevant variables added to the model, the following formula is recommended in the case of multiple regression:
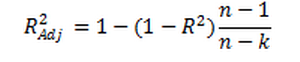
where n is the sample size, and k is number of the estimated parameters in our model.
Back to our earlier Excel results for the multiple regression model estimated for the apartment example, we can see that while the R2 has been inflated from .504 to .612 due to the new added factor, apartment size, the adjusted R2 has dropped the inflated value to .526. To understand it better, you should pay attention to the associated p-value for the newly added factor. Since this value is more than .05, we cannot reject the hypothesis that the true coefficient of apartment size (area) is significantly different from zero. In other words, in its current situation, apartment size is not a significant factor, yet the value of R2 has been inflated!
Furthermore, the adjusted R2 indicates that only 61.2% of variations in price of one-bedroom apartments in Nelson, BC, can be explained by their locations and sizes. Almost 40% of the variations of the price still cannot be explained by these two factors. One may seek to improve this model, by searching for more relevant factors such as style of the apartment, year built, etc. and add them in to this model.
Using the interactive Excel template shown in Figure 8.8, you can estimate a multiple regression model. Again, enter your data into the yellow cells only. For this template you are allowed to use up to 50 observations for each column. Like all other interactive templates in this textbook, you use special paste/values when you paste your data from other spreadsheets. Specifically, if you have fewer than 50 data entries, you must also fill out the rest of the empty yellow cells under X1, X2, and Y with zeros. Now, select your alpha level. By clicking enter, you will not only have all your estimated coefficients along with their t-values, etc., you will also be guided as to whether the model is significant both overall and individually. If your p-value associated with F-value within the ANOVA table is not less than the selected alpha level, you will see a message indicating that your estimated model is not overall significant, and as a result, no values for C.I. and P.I. will be shown. By either changing the alpha level and/or adding more accurate data, it is possible to estimate a more significant multiple regression model.
An interactive or media element has been excluded from this version of the text. You can view it online here: https://opentextbc.ca/introductorybusinessstatistics/?p=118
Figure 8.8 Interactive Excel Template for Multiple Regression Model – see Appendix 8.
One more point is about the format of your assumed multiple regression model. You can see that the nature of the associations between the dependent variable and all the independent variables may not always be linear. In reality, you will face cases where such relationships may be better formed by a nonlinear model. Without going into the details of such a non-linear model, just to give you an idea, you should be able to transform your selected data for X1, X2, and Y before estimating your model. For instance, one possible multiple regression non-linear model may be a model in which both the dependent and independent variables have been transformed to a natural logarithm rather than a level. In order to estimate such a model within Figure 8.5, all you need to do is transform the data in all three columns in a separate sheet from level to logarithm. In doing this, simply use =log(say A1) where in cell A1 you have the first observation of X1, and =log(say B1),…. Finally, simply cut and special paste/value into the yellow columns within the template. Now you have estimated a multiple regression model with both sides in a non-linear form (i.e., log form).
Predictions using the estimated simple regression
If the estimated regression line fits well into the data, the model can then be used for predictions. Using the above estimated simple regression model, we can predict the price of an apartment a given distance to downtown. This is known as the prediction interval or P.I. Alternatively, we may predict the mean price of the apartment, also known as the confidence interval or C.I., for the mean value.
In predicting intervals for the price of an apartment that is six kilometres away from downtown, we simply set x=6 , and substitute it back into the estimated equation:

You should pay attention to the scale of data. In this case, the dependent variable is measured in $1000s. Therefore, the predicted value for an apartment six kilometres from downtown is 39.56*1000=$39,560. This value is known as the point estimate of the prediction and is not reliable, as we are not clear how close this value is to the true value of the population.
A more reliable estimate can be constructed by setting up an interval around the point estimate. This can be done in two ways. We can predict the particular value of y for a given value of x, or we can estimate the expected value (mean) of y, for a given value of x. For the particular value of y, we use the following formula for the interval:
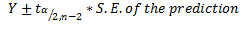
where the standard error, S.E., of the prediction is calculated based on the following formula:
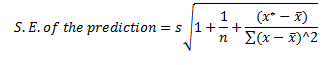
In this equation, x* is the particular value of the independent variable, which in our case is 6, and s is the standard error of the regression, calculated as:
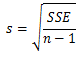
From the Excel printout for the simple regression model, this standard error is estimated as 7.02.
The sum of squares of the independent variable,
can also be calculated as shown in Figure 8.9.
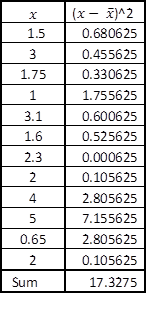
Figure 8.9
All these calculated values can be substituted back into the formula for the S.E. of the prediction:
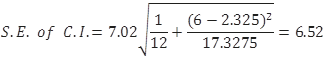
Now that the S.E. of the confidence interval has been calculated, you can pick up the cut-off point from the t-table. Given the degrees of freedom 12-2=10, the appropriate value from the t-table is 2.23. You use this information to calculate the margin of error as 6.52*2.23=14.54. Finally, construct the prediction interval for the particular value of the price of an apartment located six kilometres away from downtown as:
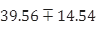
This is a compact version of the prediction interval. For a more general version of any confidence interval for any given confidence level of alpha, we can write:
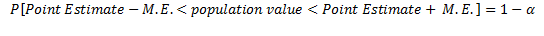
Intuitively, for say a .05 level of confidence, we are 95% confident that the true parameter of the population will be within these two lower and upper limits:
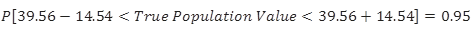
Based on our simple regression model that only includes distance as a significant factor in predicting the price of an apartment, and for a particular apartment six kilometres away from downtown, we are 95% confident that the true price of an apartments in Nelson, BC, is between $25,037 and $54,096, with a width of $29,059. One should not be surprised there is such a wide width, given the fact that the coefficient of determination of this model was only 50%, and the fact that we have selected a distance far away from the mean distance from downtown. We can always improve these numbers by adding more explanatory variables to our simple regression model. Alternatively, we can predict only for the numbers as much as possible close to the downtown area.
Now we estimate the expected value (mean) of y for a given value of x, the so-called prediction interval. The process of constructing intervals is very similar to the previous case, except we use a new formula for S.E. and of course we set up the intervals for the mean value of the apartment price (i.e., =59.33).
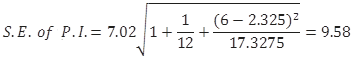
You should be very careful to note the difference between this formula and the one introduced earlier for S.E. for predicting the particular value of y for a given value of x. They look very similar but this formula comes with an extra 1 inside the radical!
The margin of error is then calculated as 2.179*3.82=8.32. We use this to set up directly the lower and upper limits of the estimates:
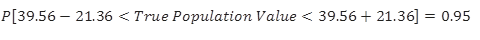
Thus, for the average price of apartments located in Nelson, BC, six kilometres away from downtown, we are 95% confident that this average price will be between $18,200 and $60,920, with a width of $47,720. Compared with the earlier width for C.I., it is obvious that we are less confident in predicting the average price. The reason is that the S.E. for the prediction is always larger than the S.E. for the confidence interval.
This process can be repeated for all different levels of x, to calculate the associated confidence and prediction intervals. By doing this, we will have a range of lower and upper levels for both P.I.s and C.I.s. All these numbers can be reproduced within the interactive Excel template shown in Figure 8.8. If you use a statistical software such as Minitab, you will directly plot a scatter diagram with all P.I.s and C.I.s as well as the estimated linear regression line all in one diagram. Figure 8.10 shows such a diagram from Minitab for our example.
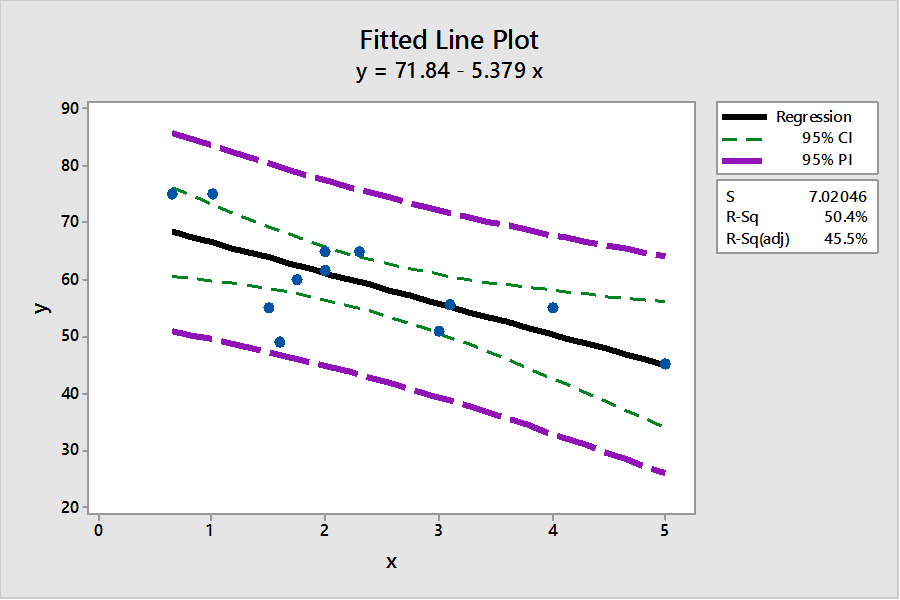
Figure 8.10 Minitab Plot for C.I. and P.I.
Figure 8.10 indicates that a more reliable prediction should be made as close as possible to the mean of our observations for x. In this graph, the widths of both intervals are at the lowest levels closer to the means of x and y.
You should be careful to note that Figure 8.10 provides the predicted intervals only for the case of a simple regression model. For the multiple regression model, you may use other statistical software packages, such as SAS, SPSS, etc., to estimate both P.I. and C.I. For instance, by selecting x1=3, and x2=300, and coding these figures into Minitab, you will see the results as shown in Figure 8.11. Alternatively, you may use the interactive Excel template provided in Figure 8.8 to estimate your multiple regression model, and to check for the significance of the estimated parameters. This template can also be used to construct both the P.I. and C.I. for the given values of x1=3, and x2=300 or any other values of your choice. Furthermore, this template enables you to test if the estimated multiple regression model is overall significant. When the estimated multiple regression model is not overall significant, this template will not provide the P.I. and C.I. To practice this case, you may want to change the yellow columns of x1 and x2 with different random numbers that are not correlated with the dependent variable. Once the estimated model is not overall significant, no prediction values will be provided.
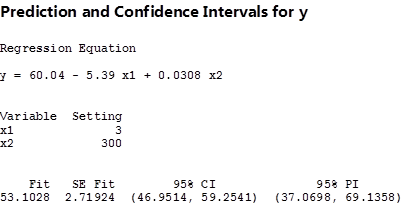
Figure 8.11
The 95% C.I., and P.I. figures in the brackets are the lower and upper limits of the intervals given the specific values for distance and size of apartments. The fitted value of the price of apartment, as well as the standard error of this value, are also estimated.
We have just given you some rough ideas about how the basic regression calculations are done. We left out other steps needed to calculate more detailed results of regression without a computer on purpose, for you will never compute a regression without a computer (or a high-end calculator) in all of your working years. However, by working with these interactive templates, you will have a much better chance to play around with any data to see how the outcomes can be altered, and to observe their implications for the real-world business decision-making process.
Correlation and covariance
The correlation between two variables is important in statistics, and it is commonly reported. What is correlation? The meaning of correlation can be discovered by looking closely at the word—it is almost co-relation, and that is what it means: how two variables are co-related. Correlation is also closely related to regression. The covariance between two variables is also important in statistics, but it is seldom reported. Its meaning can also be discovered by looking closely at the word—it is co-variance, how two variables vary together. Covariance plays a behind-the-scenes role in multivariate statistics. Though you will not see covariance reported very often, understanding it will help you understand multivariate statistics like understanding variance helps you understand univariate statistics.
There are two ways to look at correlation. The first flows directly from regression and the second from covariance. Since you just learned about regression, it makes sense to start with that approach.
Correlation is measured with a number between -1 and +1 called the correlation coefficient. The population correlation coefficient is usually written as the Greek rho, ρ, and the sample correlation coefficient as r. If you have a linear regression equation with only one explanatory variable, the sign of the correlation coefficient shows whether the slope of the regression line is positive or negative, while the absolute value of the coefficient shows how close to the regression line the points lie. If ρ is +.95, then the regression line has a positive slope and the points in the population are very close to the regression line. If r is -.13 then the regression line has a negative slope and the points in the sample are scattered far from the regression line. If you square r, you will get R2, which is higher if the points in the sample lie very close to the regression line so that the sum of squares regression is close to the sum of squares total.
The other approach to explaining correlation requires understanding covariance, how two variables vary together. Because covariance is a multivariate statistic, it measures something about a sample or population of observations where each observation has two or more variables. Think of a population of (x,y) pairs. First find the mean of the x’s and the mean of the y’s, μx and μy. Then for each observation, find (x – μx)(y – μy). If the x and the y in this observation are both far above their means, then this number will be large and positive. If both are far below their means, it will also be large and positive. If you found Σ(x – μx)(y – μy), it would be large and positive if x and y move up and down together, so that large x’s go with large y’s, small x’s go with small y’s, and medium x’s go with medium y’s. However, if some of the large x’s go with medium y’s, etc. then the sum will be smaller, though probably still positive. A Σ(x – μx)(y – μy) implies that x’s above μx are generally paired with y’s above μy, and those x’s below their mean are generally paired with y’s below their mean. As you can see, the sum is a measure of how x and y vary together. The more often similar x’s are paired with similar y’s, the more x and y vary together and the larger the sum and the covariance. The term for a single observation, (x – μx)(y – μy), will be negative when the x and y are on opposite sides of their means. If large x’s are usually paired with small y’s, and vice versa, most of the terms will be negative and the sum will be negative. If the largest x’s are paired with the smallest y’s and the smallest x’s with the largest y’s, then many of the (x – μx)(y – μy) will be large and negative and so will the sum. A population with more members will have a larger sum simply because there are more terms to be added together, so you divide the sum by the number of observations to get the final measure, the covariance, or cov:
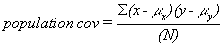
The maximum for the covariance is the product of the standard deviations of the x values and the y values, σxσy. While proving that the maximum is exactly equal to the product of the standard deviations is complicated, you should be able to see that the more spread out the points are, the greater the covariance can be. By now you should understand that a larger standard deviation means that the points are more spread out, so you should understand that a larger σx or a larger σy will allow for a greater covariance.
Sample covariance is measured similarly, except the sum is divided by n-1 so that sample covariance is an unbiased estimator of population covariance:

Correlation simply compares the covariance to the standard deviations of the two variables. Using the formula for population correlation:
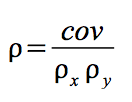
or
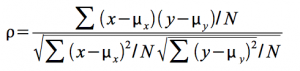
At its maximum, the absolute value of the covariance equals the product of the standard deviations, so at its maximum, the absolute value of r will be 1. Since the covariance can be negative or positive while standard deviations are always positive, r can be either negative or positive. Putting these two facts together, you can see that r will be between -1 and +1. The sign depends on the sign of the covariance and the absolute value depends on how close the covariance is to its maximum. The covariance rises as the relationship between x and y grows stronger, so a strong relationship between x and y will result in r having a value close to -1 or +1.
Covariance, correlation, and regression
Now it is time to think about how all of this fits together and to see how the two approaches to correlation are related. Start by assuming that you have a population of (x, y) which covers a wide range of y-values, but only a narrow range of x-values. This means that σy is large while σx is small. Assume that you graph the (x, y) points and find that they all lie in a narrow band stretched linearly from bottom left to top right, so that the largest y’s are paired with the largest x’s and the smallest y’s with the smallest x’s. This means both that the covariance is large and a good regression line that comes very close to almost all the points is easily drawn. The correlation coefficient will also be very high (close to +1). An example will show why all these happen together.
Imagine that the equation for the regression line is y=3+4x, μy = 31, and μx = 7, and the two points farthest to the top right, (10, 43) and (12, 51), lie exactly on the regression line. These two points together contribute ∑(x–μx)(y–μy) =(10-7)(43-31)+(12-7)(51-31)= 136 to the numerator of the covariance. If we switched the x’s and y’s of these two points, moving them off the regression line, so that they became (10, 51) and (12, 43), μx, μy, σx, and σy would remain the same, but these points would only contribute (10-7)(51-31)+(12-7)(43-31)= 120 to the numerator. As you can see, covariance is at its greatest, given the distributions of the x’s and y’s, when the (x, y) points lie on a straight line. Given that correlation, r, equals 1 when the covariance is maximized, you can see that r=+1 when the points lie exactly on a straight line (with a positive slope). The closer the points lie to a straight line, the closer the covariance is to its maximum, and the greater the correlation.
As the example in Figure 8.12 shows, the closer the points lie to a straight line, the higher the correlation. Regression finds the straight line that comes as close to the points as possible, so it should not be surprising that correlation and regression are related. One of the ways the goodness of fit of a regression line can be measured is by R2. For the simple two-variable case, R2 is simply the correlation coefficient r, squared.
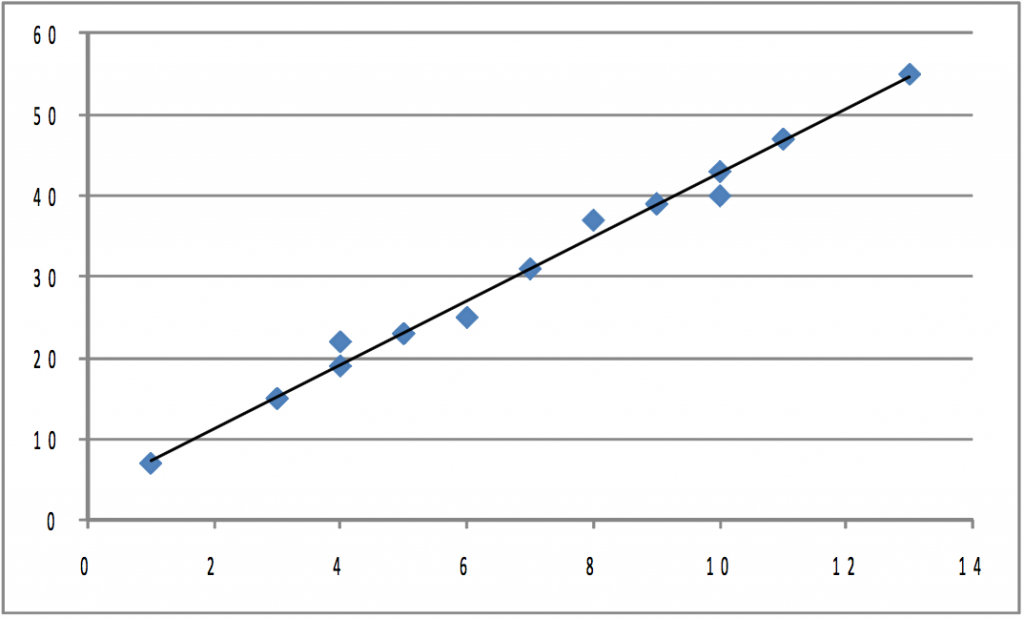
Figure 8.12 Plot of Initial Population
Correlation does not tell us anything about how steep or flat the regression line is, though it does tell us if the slope is positive or negative. If we took the initial population shown in Figure 8.12, and stretched it both left and right horizontally so that each point’s x-value changed, but its y-value stayed the same, σx would grow while σy stayed the same. If you pulled equally to the right and to the left, both μx and μy would stay the same. The covariance would certainly grow since the (x–μx) that goes with each point would be larger absolutely while the (y–μy)’s would stay the same. The equation of the regression line would change, with the slope b becoming smaller, but the correlation coefficient would be the same because the points would be just as close to the regression line as before. Once again, notice that correlation tells you how well the line fits the points, but it does not tell you anything about the slope other than if it is positive or negative. If the points are stretched out horizontally, the slope changes but correlation does not. Also notice that though the covariance increases, correlation does not because σx increases, causing the denominator in the equation for finding r to increase as much as covariance, the numerator.
The regression line and covariance approaches to understanding correlation are obviously related. If the points in the population lie very close to the regression line, the covariance will be large in absolute value since the x’s that are far from their mean will be paired with y’s that are far from theirs. A positive regression slope means that x and y rise and fall together, which also means that the covariance will be positive. A negative regression slope means that x and y move in opposite directions, which means a negative covariance.
Summary
Simple linear regression allows researchers to estimate the parameters — the intercept and slopes — of linear equations connecting two or more variables. Knowing that a dependent variable is functionally related to one or more independent or explanatory variables, and having an estimate of the parameters of that function, greatly improves the ability of a researcher to predict the values the dependent variable will take under many conditions. Being able to estimate the effect that one independent variable has on the value of the dependent variable in isolation from changes in other independent variables can be a powerful aid in decision-making and policy design. Being able to test the existence of individual effects of a number of independent variables helps decision-makers, researchers, and policy-makers identify what variables are most important. Regression is a very powerful statistical tool in many ways.
The idea behind regression is simple: it is simply the equation of the line that comes as close as possible to as many of the points as possible. The mathematics of regression are not so simple, however. Instead of trying to learn the math, most researchers use computers to find regression equations, so this chapter stressed reading computer printouts rather than the mathematics of regression.
Two other topics, which are related to each other and to regression, were also covered: correlation and covariance.
Something as powerful as linear regression must have limitations and problems. There is a whole subject, econometrics, which deals with identifying and overcoming the limitations and problems of regression.